题目内容
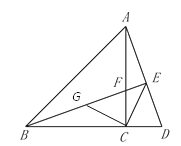
【题目】如图,在△ABC中,AC=BC,∠ACB=![]() ,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
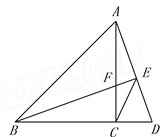
(1)求证: CF=CD;
(2)求证: ![]() ;
;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
【答案】(1)证明见解析(2)证明见解析(3)AE,BE,CE之间满足的等量关系![]()
【解析】试题分析:(1)由垂直的定义得到∠ACB=90°,根据全等三角形的判定定理ASA可证明△BCF≌△ACD,然后根据全等三角形的性质可证明;
(2)根据相似三角形的判定证得△BED∽△ACD,然后根据相似三角形的性质可证明;
(3)在BE上截取BG=AE,连接CG,然后根据三角形全等的判定可证明△GCE是等腰直角三角形,由此可得到结果.
试题解析:(1)证明:∵∠BCA=∠ACD = 90°
∴∠FBC+∠D=∠CAD +∠D = 90°
∴∠FBC =∠CAD
∵AC=BC
∴△BCF≌△ACD(ASA)
∴CF=CD
(2)证明:∵∠FBC =∠CAD ∠D=∠D
∴△BED∽△ACD
∴BD:AD=ED:CD
∴![]()
(3)AE,BE,CE之间满足的等量关系![]()
理由:在BE上截取BG=AE,连接CG,
∵∠FBC =∠CAD BC=AC
∴△BCG≌△ACE
∴GC=EC 且∠BCG=∠ACE
∴∠GCE=∠ACD= 90°
∴△GCE为等腰直角三角形
∴GC=![]() CE
CE
∴![]()

练习册系列答案
相关题目