Question

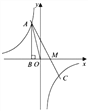
【题目】如图，已知反比例函数的图象经过第二象限内的点A（，4），AB⊥x轴于点B，△AOB的面积为2,若直线经过点A，并且经过反比例函数的图象上另一点C（2，）．

（1）求反比例函数和直线的解析式；

（2）设直线与轴交于点M，求AM的长．

Answer 1

【答案】(1) ，y=﹣2x+2；(2)2

【解析】分析：

（1）由题意易得S△AOB=AB·，这样结合已知条件即可求得m的值，从而可得点A的坐标，由点A的坐标求得k的值，即可得到反比例函数的解析式，再将点C的坐标代入所得的解析式求得n的值，可得点C的坐标，这样由直线过点A、C即可求得一次函数的解析式了；

（2）由（1）中所得一次函数的解析式求得点M的坐标，由此可得BM的长，这样结合AB的长即可由勾股定理求得AM的长了.

（1）∵点A（m，4）在第二象限，即AB=4，OB=|m|,

∵S△AOB=AB·OB=AB·，

解得： |m|=1，

∴A (-1，4)

∵点A（-1，4）在反比例函数的图像上

∴k=-4，

∴反比例函数解析式为，

又∵反比例函数的图象经过C（2，n）

∴n=-2，

∴C （2，﹣2），

∵直线y=ax+b过点A （﹣1，4），C （2，﹣2）

∴ ,

解方程组得： ，

∴直线y=ax+b的解析式为y=﹣2x+2；

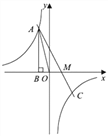
（2）当y=0时，即﹣2x+2=0，

解得x=1，

∴点M的坐标是M（1，0），

在Rt△ABM中，∵AB=4，BM=BO+OM=1+1=2，

∴AM=.