题目内容
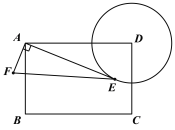
【题目】如图,已知AB为⊙O的直径,弦CD⊥AB,垂足为H.
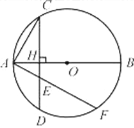
(1) 求证:AH![]() AB=AC2;
AB=AC2;
(2) 若过A的直线与弦CD(不含端点)相交于点E,与⊙O相交于点F,求证:AE![]() AF=AC2;
AF=AC2;
(3) 若过A的直线与直线CD相交于点P,与⊙O相交于点Q,判断AP![]() AQ=AC2是否成立(不必证明).
AQ=AC2是否成立(不必证明).
【答案】(1)详见解析;(2)详见解析;(3)成立.
【解析】
(1)连接CB,证明△CAH∽△BAC即可;
(2)连接CF,证△AEC∽△ACF,根据射影定理即可证得;
(3)由(1)(2)的结论可知,APAQ=AC2成立.
(1) 连结CB,∵AB是⊙O的直径,∴∠ACB=90°.
而∠CAH=∠BAC,∴△CAH∽△BAC .
∴![]() , 即AH
, 即AH![]() AB=AC2 .
AB=AC2 .
(2) 连结FB,易证△AHE∽△AFB,
∴ AE![]() AF=AH
AF=AH![]() AB,
AB,
∴ AE![]() AF=AC2 .
AF=AC2 .
(也可连结CF,证△AEC∽△ACF)
(3) 结论AP![]() AQ=AC2成立 .
AQ=AC2成立 .

 阅读快车系列答案
阅读快车系列答案【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.