题目内容
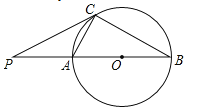
【题目】如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
(1)求证:∠PCA=∠B;
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.
【答案】(1)证明见试题解析;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
试题分析:(1)连接OC,由PC是⊙O的切线,得到∠1+∠PCA=90°,由AB是⊙O的直径,得到∠2+∠B=90°,从而得到结论;
(2)△ABQ与△ABC的面积相等时,有三种情况,即:①当∠AOQ=∠AOC=50°时;②当∠BOQ=∠AOC=50°时;③当∠BOQ=50°时,即∠AOQ=230°时;分别求得点Q所经过的弧长即可.
试题解析:(1)连接OC,∵PC是⊙O的切线,∴∠PCO=90°,∴∠1+∠PCA=90°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠2+∠B=90°,∵OC=OA,∴∠1=∠2,∴∠PCA=∠B;
(2)解:∵∠P=40°,∴∠AOC=50°,∵AB=12,∴AO=6,
①当∠AOQ=∠AOC=50°时,△ABQ与△ABC的面积相等,∴点Q所经过的弧长=![]() =
=![]() ;
;
②当∠BOQ=∠AOC=50°时,即∠AOQ=130°时,△ABQ与△ABC的面积相等,∴点Q所经过的弧长=![]() =
=![]() ;
;
③当∠BOQ=50°时,即∠AOQ=230°时,△ABQ与△ABC的面积相等,∴点Q所经过的弧长=![]() =
=![]() ;
;
综上所述,当△ABQ与△ABC的面积相等时,动点Q所经过的弧长为![]() 或
或![]() 或
或![]() .
.


练习册系列答案
相关题目