Question

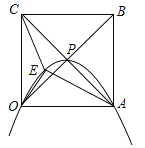
【题目】正方形OABC的边长为4，对角线相交于点P，抛物线L经过O、P、A三点，点E是正方形内的抛物线上的动点．

（1）建立适当的平面直角坐标系，①直接写出O、P、A三点坐标；

②求抛物线L的解析式；

（2）求△OAE与△OCE面积之和的最大值．

Answer 1

【答案】（1）①O（0，0），A（4，0），P（2，2）；②；（2）9．

【解析】

试题分析：（1）以O点为原点，线段OA所在的直线为x轴，线段OC所在的直线为y轴建立直角坐标系，如图所示．

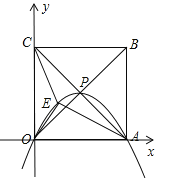
①∵正方形OABC的边长为4，对角线相交于点P，∴点O的坐标为（0，0），点A的坐标为（4，0），点P的坐标为（2，2）．

②设抛物线L的解析式为，∵抛物线L经过O、P、A三点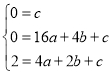，∴，解得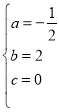：，∴抛物线L的解析式为；

（2）∵点E是正方形内的抛物线上的动点，∴设点E的坐标为（m，）（0＜m＜4），∴S△OAE+SOCE=OAyE+OCxE==，∴当m=3时，△OAE与△OCE面积之和最大，最大值为9．