题目内容
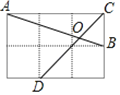
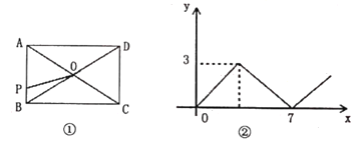
【题目】如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB-BC→CD向点D运动设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所小示,则AD的长为________.
【答案】4
【解析】
当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,结合图象可得△AOP面积最大为3,得到AB与BC的积为12;当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,得到AB与BC的和为7,构造关于AB的一元二方程可求解.
①当点P在AB上运动时,y=![]() AP·×
AP·×![]() AD
AD
由图象可知:△AOP面积逐渐增大,当P点到达B点时,△AOP面积最大为3,此时 y=![]() AB×
AB×![]() BC=
BC=![]() AB·BC=3,即AB·BC=12;
AB·BC=3,即AB·BC=12;
②当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,由图象可知,此时△AOP面积的为0,P点运动路径长为7,即AB+BC=7
∴BC=7-AB,代入ABBC=12,得:
AB(7-AB)=12,解得AB=4或3
又∵AB<AD,即AB<BC
∴AB=3,BC=4.
∴AD=4
故答案为:4

练习册系列答案
相关题目