题目内容
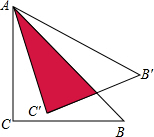
如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C′,使得点A′恰好落在AB上,连接BB′,则BB′的长度为______.
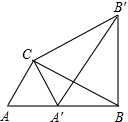

∵Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,
∴A′C=AC=1,AB=2,BC=
,
∵∠A=60°,
∴△AA′C是等边三角形,
∴AA′=
AB=1,
∴A′C=A′B,
∴∠A′CB=∠A′BC=30°,
∵△A′B′C是△ABC旋转而成,
∴∠A′CB′=90°,BC=B′C,
∴∠B′CB=90°-30°=60°,
∴△BCB′是等边三角形,
∴BB′=BC=
.
故答案为:
.

∴A′C=AC=1,AB=2,BC=
| 3 |
∵∠A=60°,
∴△AA′C是等边三角形,
∴AA′=
| 1 |
| 2 |
∴A′C=A′B,
∴∠A′CB=∠A′BC=30°,
∵△A′B′C是△ABC旋转而成,
∴∠A′CB′=90°,BC=B′C,
∴∠B′CB=90°-30°=60°,
∴△BCB′是等边三角形,
∴BB′=BC=
| 3 |
故答案为:
| 3 |


练习册系列答案
相关题目