题目内容
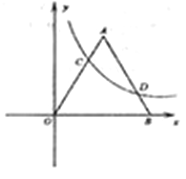
【题目】已知:如图,在平面直角坐标系![]() 中,等边
中,等边![]() 的边长为6,点
的边长为6,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() .反比例函数
.反比例函数![]() 的图象恰好经过点
的图象恰好经过点![]() 和点
和点![]() .则
.则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
【答案】A.
【解析】
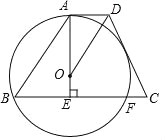
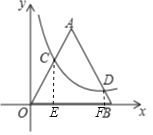
试题分析:过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,设BD=a,则OC=3a,根据等边三角形的性质结合解含30度角的直角三角形,可找出点C、D的坐标,再利用反比例函数图象上点的坐标特征即可求出a、k的值,此题得解.
过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,如图所示.
设BD=a,则OC=3a.
∵△AOB为边长为6的等边三角形,∴∠COE=∠DBF=60°,OB=6.
在Rt△COE中,∠COE=60°,∠CEO=90°,OC=3a,
∴∠OCE=30°,∴OE=![]() a,CE=
a,CE=![]() ,∴点C(
,∴点C(![]() ,
,![]() ).
).
同理,可求出点D的坐标为(6﹣![]() a,
a,![]() a).
a).
∵反比例函数![]() (k≠0)的图象恰好经过点C和点D,
(k≠0)的图象恰好经过点C和点D,
∴k=![]() ×
×![]() a=(6﹣
a=(6﹣![]() a)×
a)×![]() a,∴a=
a,∴a=![]() ,k=
,k=![]() .
.
故选A.

【题目】我市雷雷服饰有限公司生产了一款夏季服装,通过实验商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
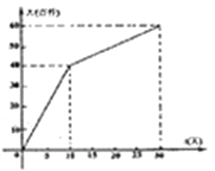
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的关系如下图所示.
为整数,单位:天)的关系如下图所示.
时间 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量 | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为![]() (百件),求
(百件),求![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 为何值时,日销售总量
为何值时,日销售总量![]() 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.