��Ŀ����
����Ŀ����7��������ijУ���ƽ��¿θĵĹ����������������ѡ���У�A��������B��������C��������D����ë����E��ƹ������ѧ���ɸ����Լ��İ���ѡ��һ����ѧУ����ʦ��ij��ȫ��ѧ����ѡ��������е���ͳ�����Ƴ���������������ͳ��ͼ����ͼ����
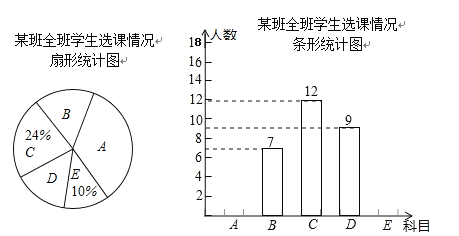
��1����������ð��������������ȫƵ���ֲ�ֱ��ͼ��
��2����ʾ���������������ε�Բ�Ľ��Ƕ��ٶȣ�
��3���ð��ί4������1��ѡ��������2��ѡ��������1��ѡ������������ʦҪ����4������ѡ2���˽����Ƕ�����ѡ�εĿ������������б�����״ͼ�ķ�������ѡ����2��ǡ��1��ѡ��������1��ѡ������ĸ�����
���𰸡���1��50��������ͼ����������2��50��4������3��![]() ��
��
��������
�����������1�������ð�������=C�������12��C��İٷֱ�24%���㼴����Ȼ�����E����A�����������ɲ�ȫͳ��ͼ����2�����������������ε�Բ�Ľ�=360���B��İٷֱȣ���3������״ͼ�����б����ó����п��ܵ�12���������ǡ��1��ѡ��������1��ѡ���������4����Ȼ����ݸ��ʹ�ʽ���㼴����
����������⣺��1���ð��������ǣ�12��24%=50��������
��E�������ǣ�50��10%=5��������
A��������50����7+12+9+5��=17��������
��ȫƵ���ֲ�ֱ��ͼ���£�
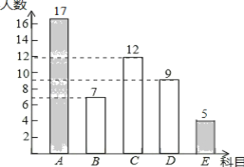
��2��![]() ��360��=50��4��
��360��=50��4��
����ʾ���������������ε�Բ�Ľ���50��4����
��3������״ͼ���£�
![]()
���б����£�

����12�ֵȿ��ܵ����������ǡ��1��ѡ��������1��ѡ���������4����
��ѡ����2��ǡ��1��ѡ��������1��ѡ�������������ǣ�![]() =
=![]() ��
��