题目内容
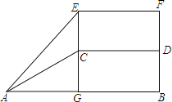
【题目】如图是扬州某商场的自动扶梯侧面示意图,已知自动扶梯AC的坡度为1:2,AC的长度为5![]() 米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.(参考数据:sin42°=
米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.(参考数据:sin42°=![]() ,cos42°=
,cos42°=![]() ,tan42°=
,tan42°=![]() )
)
【答案】(4![]() -5)米.
-5)米.
【解析】
试题分析:根据题意得出AG=2CG,根据Rt△ACG的勾股定理求出CG和AG的长度,根据tan∠EAG的值求出EG的长度,最后根据CE=EG-CG得出答案.
试题解析:根据题意得:AG=2CG, ∵∠AGE=90°, ∴由勾股定理得:CG2+AG2=AC2,
即CG2+(2CG)2=(5![]() )2, 解得:CG=5(米),
)2, 解得:CG=5(米),
∴AG=10米, ∵tan∠EAG=![]() , ∴EG=AG
, ∴EG=AG![]() tan42°,
tan42°,
∴CE=EG﹣CG=AG![]() tan42°﹣CG=10×
tan42°﹣CG=10×![]() ﹣5=4
﹣5=4![]() ﹣5(米);
﹣5(米);
答:该商场二楼的楼高CE为(4![]() ﹣5)米.
﹣5)米.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目