题目内容
如图所示，在△ABC中，∠C=90°，AB=10，AC=6，⊙O1与⊙O2是△ABC内互相外切的等圆，且分别与∠A，∠B的两边相切，则这个等圆的半径的长为______．
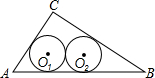
设圆的半径是r，将两圆圆心与已知的点连接．
根据勾股定理求得BC=8，
∴斜边上的高是：6×8÷10=4.8，
∴
AC•r+
BC•r+
•2r•（4.8-r）+
•r=
AC•BC，
∴r=
．
故答案为：
．
根据勾股定理求得BC=8，
∴斜边上的高是：6×8÷10=4.8，
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2r+10 |
| 2 |
| 1 |
| 2 |
∴r=
| 10 |
| 7 |
故答案为：
| 10 |
| 7 |
练习册系列答案
相关题目
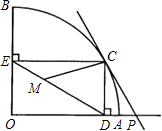点D，作CE⊥OB于点E，点M在DE上，DM=2EM，过点C的直线PC交OA的延长线于点P，且∠CPD=∠CDE．
