题目内容
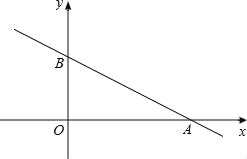
【题目】如图,在以点O为原点的直角坐标系中,一次函数y=﹣![]() x+1的图象与x轴交于A,与y轴交于点B,求:
x+1的图象与x轴交于A,与y轴交于点B,求:
(1)△AOB面积= ;
(2)△AOB内切圆半径= ;
(3)点C在第二象限内且为直线AB上一点,OC=![]() AB,反比例函数
AB,反比例函数![]() 的图象经过点C,求k的值.
的图象经过点C,求k的值.
【答案】(1)1(2)![]() (3)k=﹣
(3)k=﹣![]()
【解析】
试题分析:(1)利用一次函数的解析式分别求出A、B的坐标后,即可求出OB、OA的长度,从而可求出△AOB的面积;
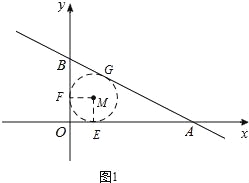
(2)设△AOB内切圆的圆心为M,⊙M与OA、OB、AB分别切于E、F、G,连接OE、OF,利用切线长定理可知BF=BG,AE=AG,设半径为r,利用AG+BG=AB列出方程即可求出r的值;
(3)利用AB的长度求出OC的长度,过点C作CD⊥x轴于点D,设点C(a,﹣![]() a+1),利用勾股定理即可求出a的值,从而求出点C的坐标,将点C代入y=
a+1),利用勾股定理即可求出a的值,从而求出点C的坐标,将点C代入y=![]() 即可求出k的值.
即可求出k的值.
试题解析:(1)令x=0代入y=﹣![]() a+1
a+1
∴y=1,
∴OB=1,
令y=0代入y=﹣![]() x+1,
x+1,
∴x=2,
∴OA=2,
S=![]() OAOB=1;
OAOB=1;
(2)设△AOB内切圆的圆心为M,
⊙M与OA、OB、AB分别切于E、F、G,
连接OE、OF,如图1,
∵∠OEM=∠MFO=∠FOE=90°,
∴四边形MFOE是矩形,
∵ME=MF,
∴矩形MFOE是正方形,
设⊙M的半径为r,
∴MF=ME=r,
由切线长定理可知:BF=BG=1﹣r,
AE=AG=2﹣r,
由勾股定理可求得:AB=![]() =
=![]() ,
,
∴AG+BG=AB,
2﹣r+1﹣r=![]() ,
,
∴r=![]() ;
;
(3)过点C作CD⊥x轴于点D,如图2,
∵OC=![]() AB,
AB,
∴OC=![]() ,
,
∵点C在直线AB上,
∴设C(a,﹣![]() a+1)(a<0),
a+1)(a<0),
∴OD=a,CD=﹣![]() a+1,
a+1,
由勾股定理可知:CD2+OD2=OC2,
∴a2+(﹣![]() a+1)2=
a+1)2=![]() ,
,
∴a=﹣![]() 或a=1(舍去)
或a=1(舍去)
∴C的坐标为(﹣![]() ,
,![]() ),
),
把C(﹣![]() ,
,![]() )代入y=
)代入y=![]() ,
,
∴k=﹣![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案

