题目内容
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=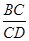 ;②四边形CGMH是矩形③△EGM≌△MHA;④S△ABC+S△CDE≥S△ACE;⑤图中的相似三角形有10对。正确结论是( )
;②四边形CGMH是矩形③△EGM≌△MHA;④S△ABC+S△CDE≥S△ACE;⑤图中的相似三角形有10对。正确结论是( )

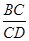 ;②四边形CGMH是矩形③△EGM≌△MHA;④S△ABC+S△CDE≥S△ACE;⑤图中的相似三角形有10对。正确结论是( )
;②四边形CGMH是矩形③△EGM≌△MHA;④S△ABC+S△CDE≥S△ACE;⑤图中的相似三角形有10对。正确结论是( )
| A.①②③④ | B.①②③⑤ | C.①③④ | D.①③⑤ |
A
∵△ABC和△CDE均为等腰直角三角形∴△ABC~△CDE∴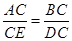
∵∠BCA=∠DCE=45°∴∠ECA=90°∴tan∠AEC=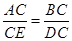 ,①结论是正确的;
,①结论是正确的;
连接CM.∵∠ECA=90°,M是AE的中点∴CM=EM∵CD=DE,DM=DM∴△CDM≌△DEM∴CDM=∠MDE=45°∵∠BCA=45°∴CH∥DM 同理可证CE∥BM∴四边形CGMH是平行四边形∵∠ECA=90°∴四边形CGMH是矩形,②结论是正确的;
∵M是AE的中点∴EM=MA∵CH∥DM∴∠GME=∠CAE同理可证∠CEM=∠HMA∴△EGM≌△MHA,③结论是正确的;
∵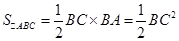 ,
,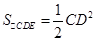 ,
,

∴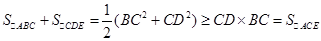 ,④结论是正确的;
,④结论是正确的;
△CDE~△ABC, △BCH~△BDM, △CDG~△BMD, △CDG~△BCH, △DGE~△CDE,
△GDE~△CDE, △DGE~△ABC, △BHA~△ABC, △BHA~△CDE, △BHA~△DGE,△BHA~△DMB等有十九对相似三角形,⑤结论是错的,故选A
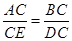
∵∠BCA=∠DCE=45°∴∠ECA=90°∴tan∠AEC=
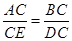 ,①结论是正确的;
,①结论是正确的;连接CM.∵∠ECA=90°,M是AE的中点∴CM=EM∵CD=DE,DM=DM∴△CDM≌△DEM∴CDM=∠MDE=45°∵∠BCA=45°∴CH∥DM 同理可证CE∥BM∴四边形CGMH是平行四边形∵∠ECA=90°∴四边形CGMH是矩形,②结论是正确的;
∵M是AE的中点∴EM=MA∵CH∥DM∴∠GME=∠CAE同理可证∠CEM=∠HMA∴△EGM≌△MHA,③结论是正确的;
∵
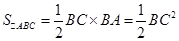 ,
,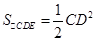 ,
,
∴
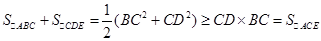 ,④结论是正确的;
,④结论是正确的;△CDE~△ABC, △BCH~△BDM, △CDG~△BMD, △CDG~△BCH, △DGE~△CDE,
△GDE~△CDE, △DGE~△ABC, △BHA~△ABC, △BHA~△CDE, △BHA~△DGE,△BHA~△DMB等有十九对相似三角形,⑤结论是错的,故选A

练习册系列答案
相关题目
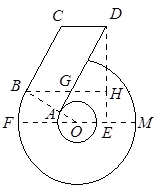

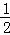
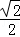
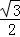


 的值是(▲)
的值是(▲)


 .
. -2cosB∣=0则∠A= 。
-2cosB∣=0则∠A= 。 ,sin60
,sin60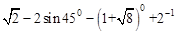 .
.