Question

在直角坐标系中，已知抛物线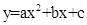与x轴交于点A(1，0)和点B，顶点为P.

 (1)若点P的坐标为（－1，4），求此时抛物线的解析式；

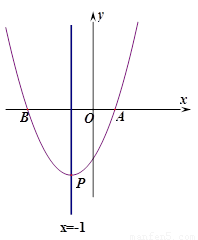
（2）如图若点P的坐标为（－1，k）,k＜0，点Q是y轴上一个动点，

当k为何值时，QB＋QP取得最小值为5；

（3）试求满足（2）时动点Q的坐标. （本题12分）

 

Answer 1

【答案】

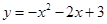；k=－3；Q点的坐标为（0，）

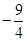【解析】

试题分析: 解：（1）由题可设抛物线解析式为将A点坐标代入，得  a=－1

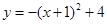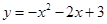∴抛物线解析式为，即。    4′

（2）作P关于y轴对称点 (1，k)，∴QP=Q。  由题意知B(－3，0)，

若QB＋QP最小，即QB＋ Q最小，则B、Q、三点共线，即B=5。

又AB=4。  连结A，得△AB是直角三角形，

则A=3。∴k=－3。    8′

（3）由（2）知，△BOQ∽△BA，

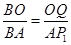∴，即。∴OQ=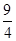

∴Q点的坐标为（0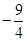，）。    12

考点：本题考查了直角三角形的性质定理

点评：此类试题难度很大，所考知识点不难，但是综合性很强，考点也很精，是常考点和必考点