题目内容
在直角坐标系中，已知点A（0，
）、B（3，0），以AB为一边作等边△ABC，且点C在第一象限．则点C的坐标是
| 3 |
（3，2
）
| 3 |
（3，2
）
，若G是△ABC的重心，则G的坐标是| 3 |
（2，
）
| 3 |
（2，
）
．| 3 |
分析：先根据锐角三角函数的定义及特殊角的三角函数值得出∠ABO=30°，则∠OBC=90°，由勾股定理求出BC，从而求出点C的坐标；根据重心的定义及性质可知G在BC的中线AD上，且AG=2GD，从而求出点G的坐标．
解答：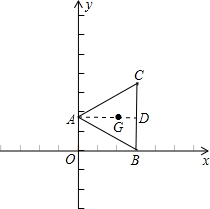
解：在△AOB中，∵∠AOB=90°，
∴tan∠ABO=OA：OB=
，
∴∠ABO=30°，
∴AB=2OA=2
．
∵△ABC是等边三角形，
∴∠ABC=60°，
∴∠OBC=∠ABO+∠ABC=90°，
∴BC=AB=AC=2
，
∴点C的坐标是（3，2
）．
过点AAD⊥BC于D，则四边形OADB是矩形，AD=OB=3，BD=OA=
，
在AD上取点G，使AG=2GD，则G是△ABC的重心．
∴AG=
AD=2，
∴G的坐标是（2，
）．
故答案为：（3，2
），（2，
）．
解：在△AOB中，∵∠AOB=90°，∴tan∠ABO=OA：OB=
| ||
| 3 |
∴∠ABO=30°，
∴AB=2OA=2
| 3 |
∵△ABC是等边三角形，
∴∠ABC=60°，
∴∠OBC=∠ABO+∠ABC=90°，
∴BC=AB=AC=2
| 3 |
∴点C的坐标是（3，2
| 3 |
过点AAD⊥BC于D，则四边形OADB是矩形，AD=OB=3，BD=OA=
| 3 |
在AD上取点G，使AG=2GD，则G是△ABC的重心．
∴AG=
| 2 |
| 3 |
∴G的坐标是（2，
| 3 |
故答案为：（3，2
| 3 |
| 3 |
点评：本题考查了锐角三角函数的定义，特殊角的三角函数值，等边三角形的性质，勾股定理，重心的性质，综合性较强，难度适中，找出点G的位置是解题的关键．
练习册系列答案
相关题目
如图，在直角坐标系中，已知直线y=kx+6与x轴、y轴分别交于A、B两点，且△ABO的面积为12．
的直角顶点的坐标为