题目内容
如图，在直角坐标系中，已知点A（-3，0），B（0，4），对△OAB连续作旋转变换，依次得到三角形①、②、③、④…，则三角形
的直角顶点的坐标为
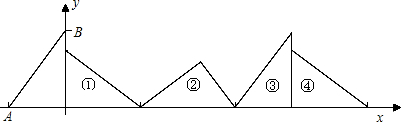
分析：先计算出AB，然后根据旋转的性质观察△OAB连续作旋转变换，得到△OAB每三次旋转后回到原来的状态，并且每三次向前移动了3+4+5=12个单位，于是判断三角形和三角形④的状态一样，然后可计算出它的直角顶点的横坐标，从而得到三角形的直角顶点的坐标．
和三角形④的状态一样，然后可计算出它的直角顶点的横坐标，从而得到三角形的直角顶点的坐标．解答：解：∵点A（-3，0），B（0，4），
∴OB=4，OA=3，
∴AB=
=5，
∵对△OAB连续作如图所示的旋转变换，
∴△OAB每三次旋转后回到原来的状态，并且每三次向前移动了3+4+5=12个单位，
而2011=3×670+1，
∴三角形和三角形④的状态一样，
所以三角形的直角顶点的横坐标为670×12=8040，纵坐标为0．
故答案为（8040，0）．
∴OB=4，OA=3，
∴AB=
| 42+32 |
∵对△OAB连续作如图所示的旋转变换，
∴△OAB每三次旋转后回到原来的状态，并且每三次向前移动了3+4+5=12个单位，
而2011=3×670+1，
∴三角形
和三角形④的状态一样，所以三角形
的直角顶点的横坐标为670×12=8040，纵坐标为0．故答案为（8040，0）．
点评：本题考查了图形旋转后的坐标问题：先要理解所旋转图形的性质，然后根据旋转的性质理解每次旋转后图形各个点的坐标变化，从中找出变化的规律，再根据规律确定某种状态下的位置及坐标．
练习册系列答案
相关题目
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．
，2）．画出△ABC的两个位似图形△A1B1C1，△A2B2C2，同时满足下列两个条件：