题目内容
在直角坐标系中，已知点A（-3，0），B（0，-4），C（0，1），过点C作直线DC交x轴于点D，使得以D、C、O为顶点的三角形与△AOB相似，这样的直线一共可以作出（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
分析：先画出草图，△AOB已确定，两直角边的比为3：4，要使以D、C、O为顶点的三角形与△AOB相似，则△COD的两直角边的比为3：4即可．
解答：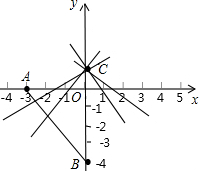
解：∵A（-3，0），B（0，-4），C（0，1），
∴OA=3，OB=4，OC=1，
∵△COD∽△AOB，
∴
=
或
=
，
∴OD=±
或
，
∴点D的坐标为（
，0）（-
，0）（
，0）（-
，0），
如图：
共有这样的直线4条．
故选D．
解：∵A（-3，0），B（0，-4），C（0，1），∴OA=3，OB=4，OC=1，
∵△COD∽△AOB，
∴
| OC |
| OD |
| 3 |
| 4 |
| OC |
| OD |
| 4 |
| 3 |
∴OD=±
| 3 |
| 4 |
| 4 |
| 3 |
∴点D的坐标为（
| 3 |
| 4 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
如图：
共有这样的直线4条．
故选D．
点评：本题考查了相似三角形的判定和坐标与图形的性质，分类讨论是解此题的关键．
练习册系列答案
相关题目
如图，在直角坐标系中，已知直线y=kx+6与x轴、y轴分别交于A、B两点，且△ABO的面积为12．
的直角顶点的坐标为