��Ŀ����
����Ŀ������������һ�ַdz���Ҫ����ѧ���������һ�����ṩ����֪�����а���������������ǿ��Է�������������.���磺��֪��A��B��C��һ��ֱ���ϣ���AB=8��BC=3��AC��Ϊ���٣�
ͨ���������Ƿ��֣������������������֣��������C�ڵ�B���Ҳ�ʱ����ͼ1����ʱ��AC=11��

����ڵ���C�ڵ�B�����ʱ�� ��ͼ2��ʱ��AC=5.

��������Ľ���˼·�������������:
���⣨1��: ��ͼ,�����ϵ�A�͵�B��ʾ�����ֱ���-1��2����C��������һ�㣬��BC=2AB�����C��ʾ������.
![]()
����(2): ��![]() ��
��![]() ��
��![]() ��ֵ.
��ֵ.
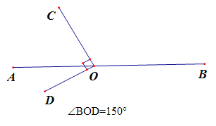
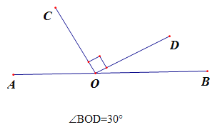
����(3): ��O��ֱ��AB��һ�㣬��OΪ�˵�������OC��OD��ʹ![]() ��
��![]() ����
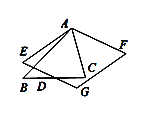
����![]() �Ķ���������ͼ�Σ�ֱ��д�������.
�Ķ���������ͼ�Σ�ֱ��д�������.
![]()
���𰸡����⣨1)��C��ʾ������8��-4�����⣨2��![]() ��ֵΪ1��-1��5��-5�����⣨3��
��ֵΪ1��-1��5��-5�����⣨3��![]() ,
, ![]() ��������.
��������.
��������
���⣨1)����������������ۣ���C��B������Լ���C��B���Ҳ࣬������BC=2AB���з�������.
���⣨2������![]() ��
��![]() �õ�
�õ�![]() ���ٽ��з������۴���x��y��ֵ.
���ٽ��з������۴���x��y��ֵ.
���⣨3���������⻭��ͼ�Σ����ýǵĺͲ��ϵ���м��㣬ֱ��д����.
�⣺���⣨1) ��C��������һ�㣬��BC=2AB����������֪��C��B������Լ���C��B���Ҳ�ֱ�Ϊ-4��8.
����(2����![]() ��
��![]() ��
��![]()
�����x=2��y=3ʱ��![]() =5��
=5��
�����x=2��y=-3ʱ��![]() =-1��
=-1��
����� ��x=-2��y=3ʱ��![]() =1��
=1��
����� ��x=-2��y=-3ʱ��![]() =-5��
=-5��
���ԣ�![]() ��ֵΪ1��-1��5��-5.
��ֵΪ1��-1��5��-5.
������