题目内容
【题目】已知:![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,连接
,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
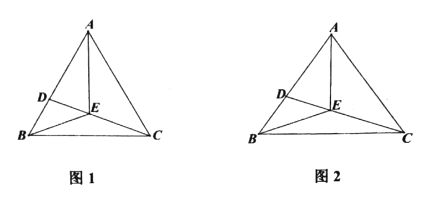
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,在不添加任何辅助线的情况下,请直接写出图中所有底角为
,在不添加任何辅助线的情况下,请直接写出图中所有底角为![]() 的等腰三角形.
的等腰三角形.
【答案】(1)见解析;(2)△ABE,△ACE,△DBE
【解析】
(1)先根据SSS证明△ABE≌△ACE,证得∠DBE=∠ACD,再根据三角形外角的性质,得出∠DBE=∠DEB,即可证出结论.
(2)计算出相关角度,根据等角对等边即可判定
∵AE平分∠BAC ∴∠BAE=∠CAE
∵AB=AC ∠BAE=∠CAE AE=AE
∴△ABE≌△ACE ,∴∠DBE=∠ACD
∵∠ADC=2∠ACD ∴∠ADC=2∠DBE
∵∠ADC=∠DBE+∠DEB ∴∠DBE=∠DEB
∴BD=ED
(2)在![]() 中,∵
中,∵![]() ,
,![]() .
.
∴∠ADC=![]() , ∠ACD=
, ∠ACD=![]() ,由(1)知:∠DBE=∠ACD
,由(1)知:∠DBE=∠ACD
∴∠DBE=∠ACD=![]() , ∴∠DBE=∠DEB=
, ∴∠DBE=∠DEB=![]()
∴△DBE是底角为![]() 的等腰三角形.
的等腰三角形.
∵AE平分∠BAC ∠ADC=![]() ,
,
∴∠BAE=∠CAE![]() DBE=∠DEB
DBE=∠DEB
∴△ABE和△ACE是底角为![]() 的等腰三角形.
的等腰三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目