题目内容
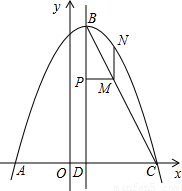
如图,抛物线y=ax2+bx+ (a≠0)经过A(-3,0)、C(5,0)两点,点B为抛物线的顶点,抛物线的对称轴与x轴交于点D.
(a≠0)经过A(-3,0)、C(5,0)两点,点B为抛物线的顶点,抛物线的对称轴与x轴交于点D.(1)求此抛物线的解析式;
(2)动点P从点B出发,沿线段BD向终点D作匀速运动,速度为每秒1个单位长度,运动时间为ts,过点P作PM⊥BD交BC于点M,过点M作MN∥BD,交抛物线于点N.
①当t为何值时,线段MN最长;
②在点P运动的过程中,是否有某一时刻,使得以O、P、M、C为顶点的四边形为等腰梯形?若存在,求出此刻的t值;若不存在,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是
 .
.
【答案】分析:(1)利用待定系数法直接将A(-3,0)、C(5,0)两点代入抛物线y=ax2+bx+ (a≠0)就可以求出抛物线的解析式.
(a≠0)就可以求出抛物线的解析式.
(2)①延长NM交AC于E,根据抛物线的解析式就可以求出顶点坐标B,利用条件得出三角形相似,求出MP,再根据矩形的性质求出点E,点N的坐标,把MN的长度表示出来,在转化 为顶点式就可以求出结论了.
②根据等腰梯形的性质连接PD,只要OD=CE时,就可以求出t值了.
解答:解:(1)∵抛物线y=ax2+bx+ 与x轴交于点A(-3,0),C(5,0)
与x轴交于点A(-3,0),C(5,0)
∴
解得 .
.
∴抛物线的函数关系式为y=- x2+x+
x2+x+ .
.
(2)①延长NM交AC于E,
∵B为抛物线y=- x2+x+
x2+x+ 的顶点,
的顶点,
∴B(1,8).(5分)
∴BD=8,OD=1.
∵C(5,0),
∴CD=4.
∵PM⊥BD,BD⊥AC,
∴PM∥AC.
∴∠BPM=∠BDC=90°,∠BMP=∠BCD.
∴△BPM∽△BDC.
∴ =
= .
.
根据题意可得BP=t,
∴ =
= .
.
∴PM= t.
t.
∵MN∥BD,PM∥AC,∠BDC=90°,
∴四边形PMED为矩形.
∴DE=PM= t.
t.
∴OE=OD+DE=1+ t.
t.
∴E(1+ t,0).
t,0).
∵点N在抛物线上,横坐标为1+ t,
t,
∴点N的纵坐标为- (1+
(1+ t)2+(1+
t)2+(1+ t)+
t)+ .
.
∴NE=- (1+
(1+ t)2+(1+
t)2+(1+ t)+
t)+
=- t2+8.
t2+8.
∵PB=t,PD=ME,
∴EM=8-t.
∴MN=NE-EM=- t2+8-(8-t)
t2+8-(8-t)
=- (t-4)2+2.
(t-4)2+2.
当t=4时,MN最大=2.
②存在符合条件的t值.
连接OP,如图(2).
若四边形OPMC是等腰梯形,只需OD=EC.
∵OD=1,DE=PM= t,
t,
∴EC=5-( t+1).
t+1).
∴5-( t+1)=1.
t+1)=1.
解得t=6.
∴当t=6时,四边形OPMC是等腰梯形.

点评:本题是一道二次函数的综合试题,考查了二次函数的最值,待定系数法求函数的解析式,等腰梯形的判定及性质,相似三角形的判定及性质.
 (a≠0)就可以求出抛物线的解析式.
(a≠0)就可以求出抛物线的解析式.(2)①延长NM交AC于E,根据抛物线的解析式就可以求出顶点坐标B,利用条件得出三角形相似,求出MP,再根据矩形的性质求出点E,点N的坐标,把MN的长度表示出来,在转化 为顶点式就可以求出结论了.
②根据等腰梯形的性质连接PD,只要OD=CE时,就可以求出t值了.
解答:解:(1)∵抛物线y=ax2+bx+
 与x轴交于点A(-3,0),C(5,0)
与x轴交于点A(-3,0),C(5,0)∴

解得
 .
.∴抛物线的函数关系式为y=-
 x2+x+
x2+x+ .
.(2)①延长NM交AC于E,
∵B为抛物线y=-
 x2+x+
x2+x+ 的顶点,
的顶点,∴B(1,8).(5分)
∴BD=8,OD=1.
∵C(5,0),
∴CD=4.
∵PM⊥BD,BD⊥AC,
∴PM∥AC.
∴∠BPM=∠BDC=90°,∠BMP=∠BCD.
∴△BPM∽△BDC.
∴
 =
= .
.根据题意可得BP=t,
∴
 =
= .
.∴PM=
 t.
t.∵MN∥BD,PM∥AC,∠BDC=90°,
∴四边形PMED为矩形.
∴DE=PM=
 t.
t.∴OE=OD+DE=1+
 t.
t.∴E(1+
 t,0).
t,0).∵点N在抛物线上,横坐标为1+
 t,
t,∴点N的纵坐标为-
 (1+
(1+ t)2+(1+
t)2+(1+ t)+
t)+ .
.∴NE=-
 (1+
(1+ t)2+(1+
t)2+(1+ t)+
t)+
=-
 t2+8.
t2+8.∵PB=t,PD=ME,
∴EM=8-t.
∴MN=NE-EM=-
 t2+8-(8-t)
t2+8-(8-t)=-
 (t-4)2+2.
(t-4)2+2.当t=4时,MN最大=2.
②存在符合条件的t值.
连接OP,如图(2).
若四边形OPMC是等腰梯形,只需OD=EC.
∵OD=1,DE=PM=
 t,
t,∴EC=5-(
 t+1).
t+1).∴5-(
 t+1)=1.
t+1)=1.解得t=6.
∴当t=6时,四边形OPMC是等腰梯形.

点评:本题是一道二次函数的综合试题,考查了二次函数的最值,待定系数法求函数的解析式,等腰梯形的判定及性质,相似三角形的判定及性质.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
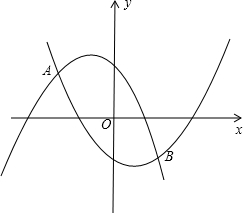 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?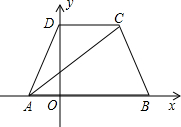 O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1.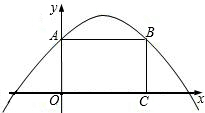 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,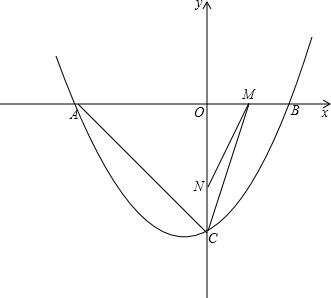 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).