题目内容
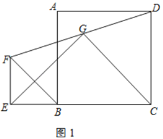
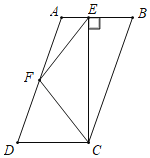
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,以CD为直径作⊙O分别交AC,BC于点E,F,过点E作⊙O的切线,分别交直线BC,AB于点H,G.
(1)求证:HG=GB;
(2)若⊙O的直径为4,连接OG,交⊙O于点M.填空:
①连接OE,ME,DM.当EG=____时,四边形OEMD为菱形;
②连接OE.当EG=_________时,四边形OEAG为平行四边形.

【答案】(1)见解析;(2)①![]() ;②2
;②2
【解析】
(1)如图连接![]() ,由相切及
,由相切及![]() 可得
可得![]() ,由
,由![]() ,可得
,可得![]() ,由于
,由于![]() 是斜边
是斜边![]() 上的高,可得
上的高,可得![]() ,即可得:
,即可得:![]() ;
;
(2) ①连接ED,可得OC=OE=OM=OD=2,假设四边形OEMD是菱形,则OE=EM,可得△OEM是等边三角形,故∠EOG=60°,可证∠EGO=30°故OG=2EO==4,利用勾股定理可得:![]() 进行计算即可;
进行计算即可;
②连接OE,当![]() ,四边形OEAG为平行四边形, 由O为直径CD的中点,
,四边形OEAG为平行四边形, 由O为直径CD的中点,![]() ,可得E为直径AC的中点,G为直径AD的中点,故EG是△ACD的中位线,即可得出答案.
,可得E为直径AC的中点,G为直径AD的中点,故EG是△ACD的中位线,即可得出答案.
(1)证明:如图连接![]() .
.

∵![]() 与
与![]() 相切,
相切,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∵![]() 是斜边
是斜边![]() 上的高,
上的高,
∴![]()
∵![]()
∴![]()
∴![]()
(2)①连接ED,如图:
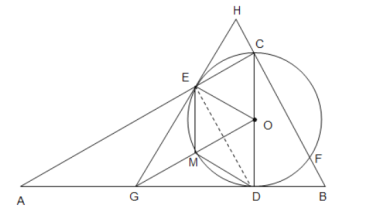
∵⊙O的直径为4,
∴⊙O的半径为2,即OC=OE=OM=OD=2,
假设四边形OEMD是菱形,则OE=EM,
又∵OE=OM,
∴OE=OM=EM,
∴△OEM是等边三角形,
∴∠EOG=60°
∵ GE与⊙O相切于E,
∴∠OEG=90°
∴∠EGO=90°-∠EOG=30°
∴OG=2EO=4,
∴![]()
∴当EG=![]() 时,四边形OEMD为菱形;
时,四边形OEMD为菱形;
故答案为:![]()
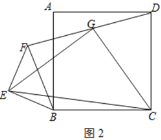
②如图,连接OE,
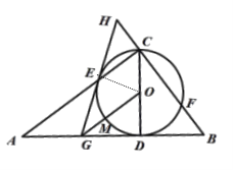
当![]() ,四边形OEAG为平行四边形
,四边形OEAG为平行四边形
∵O为直径CD的中点,![]()
∴E为直径AC的中点,G为直径AD的中点
∴EG是△ACD的中位线
∴EG=![]()
∴当EG=2时,四边形OEAG为平行四边形
故答案为:2

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】某通信公司实行的部分套餐资费标准如下:
套餐类型 | 月费 (元/月) | 套餐内包含内容 | 套餐外资费 | ||
国内数据流量(MB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
套餐1 | 18 | 100 | 0 | 0.29元/MB | 0.19元/分钟 |
套餐2 | 28 | 100 | 50 | ||
套餐3 | 38 | 300 | 50 | ||
套餐4 | 48 | 500 | 50 | ||
小明每月大约使用国内数据流量200MB,国内主叫200分钟,若想使每月付费最少,则他应预定的套餐是( )
A.套餐1B.套餐2C.套餐3D.套餐4