题目内容
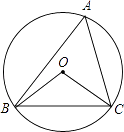
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H. 
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC= ![]() ,求AE的长.
,求AE的长.
【答案】
(1)解:DH与⊙O相切.理由如下:
连结OD、AD,如图,
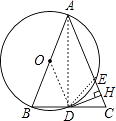
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
而AO=BO,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DH⊥AC,
∴OD⊥DH,
∴DH为⊙O的切线
(2)证明:连结DE,如图,

∵四边形ABDE为⊙O的内接四边形,
∴∠DEC=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠DEC=∠C,
∵DH⊥CE,
∴CH=EH,即H为CE的中点
(3)解:在Rt△ADC中,CD= ![]() BC=5,
BC=5,
∵cosC= ![]() =
= ![]() ,
,
∴AC=5 ![]() ,
,
在Rt△CDH中,∵cosC= ![]() =
= ![]() ,
,
∴CH= ![]() ,
,
∴CE=2CH=2 ![]() ,
,
∴AE=AC﹣CE=5 ![]() ﹣2
﹣2 ![]() =3
=3 ![]()
【解析】(1)连结OD、AD,如图,先利用圆周角定理得到∠ADB=90°,则根据等腰三角形的性质得BD=CD,再证明OD为△ABC的中位线得到OD∥AC,加上DH⊥AC,所以OD⊥DH,然后根据切线的判定定理可判断DH为⊙O的切线;(2)连结DE,如图,有圆内接四边形的性质得∠DEC=∠B,再证明∠DEC=∠C,然后根据等腰三角形的性质得到CH=EH;(3)利用余弦的定义,在Rt△ADC中可计算出AC=5 ![]() ,在Rt△CDH中可计算出CH=
,在Rt△CDH中可计算出CH= ![]() ,则CE=2CH=2
,则CE=2CH=2 ![]() , 然后计算AC﹣CE即可得到AE的长.
, 然后计算AC﹣CE即可得到AE的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目