题目内容
【题目】如图，顶点为M的抛物线y=a（x+1）2﹣4分别与x轴相交于点A，B（点A在点B的右侧），与y轴相交于点C（0，﹣3）．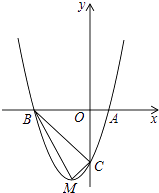
（1）求抛物线的函数表达式；
（2）判断△BCM是否为直角三角形，并说明理由．
（3）抛物线上是否存在点N（点N与点M不重合），使得以点A，B，C，N为顶点的四边形的面积与四边形ABMC的面积相等？若存在，求出点N的坐标；若不存在，请说明理由．
【答案】
（1）
解：∵抛物线y=a（x+1）2﹣4与y轴相交于点C（0，﹣3）．
∴﹣3=a﹣4，
∴a=1，
∴抛物线解析式为y=（x+1）2﹣4=x2+2x﹣3
（2）
解：△BCM是直角三角形
理由：由（1）有，抛物线解析式为y=（x+1）2﹣4，
∵顶点为M的抛物线y=a（x+1）2﹣4，
∴M（﹣1，﹣4），
由（1）抛物线解析式为y=x2+2x﹣3，
令y=0，
∴x2+2x﹣3=0，
∴x1=﹣3，x2=1，
∴A（1，0），B（﹣3，0），
∴BC2=9+9=18，CM2=1+1=2，BM2=4+16=20，
∴BC2+CM2=BM2，
∴△BCM是直角三角形
（3）
解：存在，N（﹣1+ 
， 
）或N（﹣1﹣ ， ），
∵以点A，B，C，N为顶点的四边形的面积与四边形ABMC的面积相等，且点M是抛物线的顶点，
∴①点N在x轴上方的抛物线上，
如图，
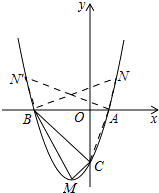
由（2）有△BCM是直角三角形，BC2=18，CM2=2，
∴BC=3 
，CM= ，
∴S△BCM= 
BC×CM= ×3 × =3，
设N（m，n），
∵以点A，B，C，N为顶点的四边形的面积与四边形ABMC的面积相等，
∴S△ABN+S△ABC=S△BCM+S△ABC，
∴S△ABN=S△BCM=3，
∵A（1，0），B（﹣3，0），
∴AB=4，
∴S△ABN= ×AB×n= ×4×n=2n=3，
∴n= ，
∵N在抛物线解析式为y=x2+2x﹣3的图象上，
∴m2+2m﹣3= ，
∴m1=﹣1+ ，m2=﹣1﹣ ，
∴N（﹣1+ ， ）或N（﹣1﹣ ， ）．
②如图2，
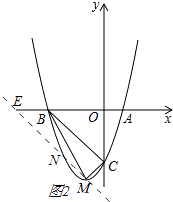
②点N在x轴下方的抛物线上，
∵点C在对称轴的右侧，
∴点N在对称轴右侧不存在，只有在对称轴的左侧，
过点M作MN∥BC，交抛物线于点N，
∵B（﹣3，0），C（0，﹣3），
∴直线BC解析式为y=﹣x﹣3，
设MN的解析式为y=﹣x+b
∵抛物线解析式为y=（x+1）2﹣4①，
∴M（﹣1，﹣4），
∴直线MN解析式为y=﹣x﹣5②，
联立①②得 
（舍）， 
，
∴N（﹣2，﹣3），
即：N（﹣1+ ， ）或N（﹣1﹣ ， ）或N（﹣2，﹣3）
【解析】（1）用待定系数法求出抛物线解析式即可；（2）由抛物线解析式确定出抛物线的顶点坐标和与x轴的交点坐标，用勾股定理的逆定理即可；（3）根据题意判断出点N只能在x轴上方的抛物线上，由已知四边形的面积相等转化出S△ABN=S△BCM ， 然后求出三角形BCM的面积，再建立关于点N的坐标的方程求解即可．
