题目内容
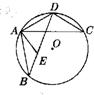 如图,已知ABCD为⊙O的内接四边形,E是BD上的一点,且有∠BAE=∠DAC.
如图,已知ABCD为⊙O的内接四边形,E是BD上的一点,且有∠BAE=∠DAC.求证:(1)△ABE∽△ACD;(2)AB•DC+AD•BC=AC•BD.
分析:(1)由圆周角定理得∠ABD=∠ACD,而∠BAE=∠DAC,即可得到△ABE∽△ACD;
(2)连接BC,由△ABE∽△ACD得,∠1=∠ADC,而∠ADC+∠ABC=180°,∠1+∠2=180°,所以∠ABC=∠2,而∠ACB=∠ADE,于是有△ABC∽△AED,得到AC•DE=AD•BC,又因为DE=BD-BE,则AC•(BD-BE)=AD•BC,即AC•BD=AC•BE+AD•BC;又由△ABE∽△ACD,得到AB•DC=AC•BE,即可得到AB•DC+AD•BC=AC•BD.
(2)连接BC,由△ABE∽△ACD得,∠1=∠ADC,而∠ADC+∠ABC=180°,∠1+∠2=180°,所以∠ABC=∠2,而∠ACB=∠ADE,于是有△ABC∽△AED,得到AC•DE=AD•BC,又因为DE=BD-BE,则AC•(BD-BE)=AD•BC,即AC•BD=AC•BE+AD•BC;又由△ABE∽△ACD,得到AB•DC=AC•BE,即可得到AB•DC+AD•BC=AC•BD.
解答:解:(1)∵∠ABD=∠ACD,
而∠BAE=∠DAC,
∴△ABE∽△ACD;
(2)连接BC,如图,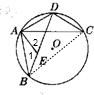
∵△ABE∽△ACD,
∴∠1=∠ADC,
而∠ADC+∠ABC=180°,∠1+∠2=180°,
∴∠ABC=∠2,
又∵∠ACB=∠ADE,
∴△ABC∽△AED,
∴AC•DE=AD•BC,
而DE=BD-BE,
∴AC•(BD-BE)=AD•BC,即AC•BD=AC•BE+AD•BC;
又由△ABE∽△ACD,
∴AB•DC=AC•BE,
∴AB•DC+AD•BC=AC•BD.
而∠BAE=∠DAC,
∴△ABE∽△ACD;
(2)连接BC,如图,

∵△ABE∽△ACD,
∴∠1=∠ADC,
而∠ADC+∠ABC=180°,∠1+∠2=180°,
∴∠ABC=∠2,
又∵∠ACB=∠ADE,
∴△ABC∽△AED,
∴AC•DE=AD•BC,
而DE=BD-BE,
∴AC•(BD-BE)=AD•BC,即AC•BD=AC•BE+AD•BC;
又由△ABE∽△ACD,
∴AB•DC=AC•BE,
∴AB•DC+AD•BC=AC•BD.
点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了圆内接四边形的性质和三角形相似的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
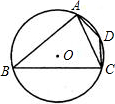 如图,已知ABCD为⊙O的内接四边形,∠B=40°,AD=CD,则∠ACD=
如图,已知ABCD为⊙O的内接四边形,∠B=40°,AD=CD,则∠ACD=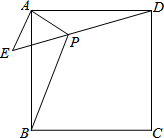 如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,且D、P、E三点共线,若EA=AP=1,PB=
如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,且D、P、E三点共线,若EA=AP=1,PB=