题目内容
（2002•泉州）如图，已知ABCD为⊙O的内接四边形，∠B=40°，AD=CD，则∠ACD= 度．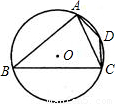
【答案】分析：根据圆内接四边形的对角互补的性质，得∠D=140°，在△ACD中，根据等腰三角形的性质以及三角形的内角和定理，得：∠CAD=∠ACD=20°．
解答：解：∵四边形ABCD是⊙O的内接四边形
∴∠B+∠D=180°
∵∠B=40°
∴∠D=140°
在△ACD中
∵
=
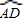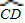
∴AD=CD
∴∠DAC=∠ACD
∵∠D=140°
∴∠ACD=∠DAC=
（180°-∠B）=20°．
点评：此题综合考查了圆内接四边形的性质、等腰三角形的性质以及三角形的内角和定理等知识的应用能力．
解答：解：∵四边形ABCD是⊙O的内接四边形
∴∠B+∠D=180°
∵∠B=40°
∴∠D=140°
在△ACD中
∵
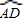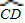
=∴AD=CD
∴∠DAC=∠ACD
∵∠D=140°
∴∠ACD=∠DAC=
（180°-∠B）=20°．点评：此题综合考查了圆内接四边形的性质、等腰三角形的性质以及三角形的内角和定理等知识的应用能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2002•泉州）如图，已知⊙O的直径BD=6，AE与⊙O相切于E点，过B点作BC⊥AE，垂足为C，连接BE、
（2002•泉州）如图，已知⊙O的直径BD=6，AE与⊙O相切于E点，过B点作BC⊥AE，垂足为C，连接BE、
