题目内容
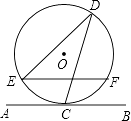
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
【答案】
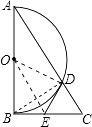
(1)证明:连接OD,OE,BD,
∵AB为圆O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE,
在△OBE和△ODE中,
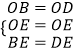 ,
,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,
则DE为圆O的切线
(2)解:在Rt△ABC中,∠BAC=30°,
∴BC= ![]() AC,
AC,
∵BC=2DE=4,
∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,
则AD=AC﹣DC=6
【解析】(1)要证切线可须连半径,再证直线和半径垂直,出现直径时,连直径的端点和圆周上一点构成90°的圆周角,进而利用斜边中线性质可证出;(2)由DE可求出BC,由30°性质可求出AB,再利用三角函数可求出AD.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
【题目】小红购买了两次笔记本,购买情况及总费用如下表
购买次数 | 购买各种笔记本的数量 | 购买总费用 | |
甲 | 乙 | ||
第一次 | 1 | 4 | 22 |
第二次 | 2 | 3 | 24 |
![]() 备注:两次购买甲、乙笔记本的单价不变
备注:两次购买甲、乙笔记本的单价不变![]()
![]() 甲、乙笔记本的单价分别是多少元?
甲、乙笔记本的单价分别是多少元?
![]() 小红第三次以相同的价格购买甲、乙两种笔记本共18本,总费用为92元,则小红第三次购买甲、乙笔记本各多少本?
小红第三次以相同的价格购买甲、乙两种笔记本共18本,总费用为92元,则小红第三次购买甲、乙笔记本各多少本?