题目内容
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
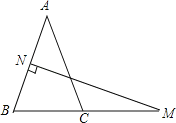
(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;
(3)你发现∠A与∠NMB有什么关系,试证明之.
【答案】(1)∠NMB=20°;(2)∠NMB =35°;(3)∠NMB=![]() ∠A,证明见解析.
∠A,证明见解析.
【解析】试题分析:(1)由在△ABC中,AB=AC,∠A=40°,根据等腰三角形的性质,可求得∠ABC的度数,又由AB的垂直平分线交AB于点N,交BC的延长线于点M,即可求得答案;
(2)由在△ABC中,AB=AC,∠A=70°,根据等腰三角形的性质,可求得∠ABC的度数,又由AB的垂直平分线交AB于点N,交BC的延长线于点M,即可求得答案;
(3)由在△ABC中,AB=AC,根据等腰三角形的性质,即可用∠A表示出∠ABC,又由AB的垂直平分线交AB于点N,交BC的延长线于点M,即可求得答案.
试题解析:(1)∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠ACB=70°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°∠ABC=20°;
(2)∵在△ABC中,AB=AC,∠A=70°,
∴∠ABC=∠ACB=55°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°∠ABC=35°;
(3)∠NMB=![]() ∠A.
∠A.
理由:∵在△ABC中,AB=AC,
∴∠ABC=∠ACB=![]() ,
,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°∠ABC=![]() ∠A.
∠A.

练习册系列答案
相关题目