题目内容
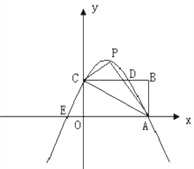
【题目】如图,在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象经过点
的图象经过点![]() ,且当
,且当![]() 和
和![]() 时所对应的函数值相等.一次函数
时所对应的函数值相等.一次函数![]() 与二次函数
与二次函数![]() 的图象分别交于
的图象分别交于![]() ,
, ![]() 两点,点
两点,点![]() 在第一象限.
在第一象限.
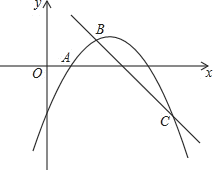
(![]() )求二次函数
)求二次函数![]() 的表达式.
的表达式.
(![]() )连接
)连接![]() ,求
,求![]() 的长.
的长.
(![]() )连接
)连接![]() ,
, ![]() 是线段
是线段![]() 得中点,将点
得中点,将点![]() 绕点
绕点![]() 旋转
旋转![]() 得到点
得到点![]() ,连接
,连接![]() ,
, ![]() ,判断四边形
,判断四边形![]() 的性状,并证明你的结论.
的性状,并证明你的结论.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】(1)根据当x=0和x=5时所对应的函数值相等,可得(5,c),根据待定系数法,可得函数解析式;
(2)联立抛物线与直线,可得方程组,根据解方程组,可得B、C 的坐标根据勾股定理,可得AB的长;
(3)根据线段中点的性质,可得M点的坐标,根据旋转的性质,可得MN与BM的关系,根据平行四边形的判定,可得答案.
解:(![]() )当
)当![]() 时
时![]() .即
.即![]() .
.
把![]()
![]() 代入解析式.
代入解析式.
 ,∴
,∴ ,
,
∴![]() .
.
(![]() )∵
)∵ ,∴
,∴![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
,
∴![]() .
.
(![]() )四边形
)四边形![]() 为矩形.
为矩形.
证:∵![]() 为
为![]() 中点,∴
中点,∴![]() .
.
又∵![]() ,∴四边形
,∴四边形![]() 为平行四边形.
为平行四边形.
又∵,∴
![]() .
.
在![]() 中.
中.
![]() .
.
∴![]() ,
,
∴四边形![]() 为矩形.
为矩形.
“点睛”本题考查了二次函数综合题,利用函数值相等得出(5,c)是解题关键,又利用了待定系数法求函数解析式;利用解方程组得出交点坐标,又利用了勾股定理;利用了平行四边形的判定;对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目
【题目】八年级一班与二班的同学在一次数学测验中的成绩统计情况如下表:
班级 | 参加人数 | 中位数 | 平均数 | 方差 |
一 | 49 | 84 | 80 | 186 |
二 | 49 | 85 | 80 | 161 |
某同学分析后得到如下结论:
①一班与二班学生平均成绩相同;
②二班优生人数多于一班(优生线85分)
③一班学生的成绩相对稳定。其中正确的是( )
A. ①② B. ①③ C. ①②③ D. ②③