题目内容
如图:在直角坐标系中,以点A(3,0)为圆心,以5为半径的圆与 轴相交于B、C两点,与
轴相交于B、C两点,与 轴相交于D、E两点.
轴相交于D、E两点.
1.若抛物线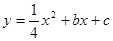 经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?(5分)
经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?(5分)
2.过点E的直线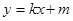 交
交 轴于F(
轴于F( ,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;(5分)
,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;(5分)
3.探索:是否能在(1)中的抛物线上找到一点Q,使直线BQ与 轴正方向所夹锐角的正切值等于
轴正方向所夹锐角的正切值等于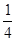 ?,若能,请直接写出Q点坐标;若不能,请说明理由. (4分)
?,若能,请直接写出Q点坐标;若不能,请说明理由. (4分)

【答案】
1.连接AE(1分)
依题意:OD=OE=4 ∴C、D两点坐标为:C(8,0),D(0,-4)(2分)
把C、D两点坐标代入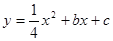 中,
中,
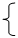 得:
得: 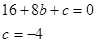 解得:
解得: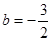
∴所求二次函数为: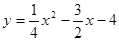 (4分)
(4分)
∵B点坐标为(-2,0)
∴当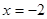 时,
时,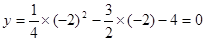 ∴点B在这条抛物线上(5分)
∴点B在这条抛物线上(5分)
2.依题意:m =4 ∴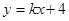
把点F(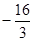 ,0)代入上式得:
,0)代入上式得: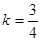
∴所求一次函数为: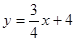 (7分)
(7分)
在Rt△OEF中,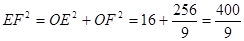 (8分)
(8分)
在△AEF中,AF=3+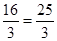 ∴
∴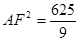
∴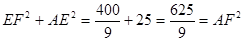 (9分)
(9分)
∴∠AEF=90º ∴EF是⊙O的切线(10分)
3.能找到这样的点Q,
其坐标分别为: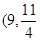 )(12分) 和 (
)(12分) 和 (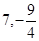 )(14分)
)(14分)
【解析】(1)据圆的圆心坐标A(3,0),以及圆的半径,可求出C点的坐标C(8,0),B点的坐标B(-2,0),然后由勾股定理,求出D点的坐标(0,-4),将C,D坐标代入抛物线的解析式中,即可求得抛物线的解析式.将B点代入,即可判断是否在抛物线上;
(2)利用两点式求出直线的解析式,然后再利用勾股定理证出∠AEF=90º,从而得出结论;
(3)利用直线BQ与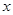 轴正方向所夹锐角的正切值等于
轴正方向所夹锐角的正切值等于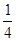 ,得出BQ直线的k值为±
,得出BQ直线的k值为±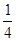 ,根据点斜式求出直线的解析式,再求它与圆的交点。
,根据点斜式求出直线的解析式,再求它与圆的交点。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: