题目内容
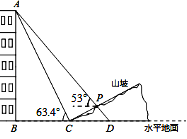
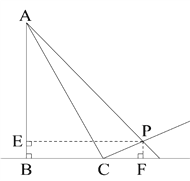
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.
(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)
(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)
(测倾器的高度忽略不计,参考数据:tan53°≈![]() ,tan63.5°≈2)
,tan63.5°≈2)
【答案】(1)此人所在P的铅直高度约为14.3米;(2)从P到点B的路程约为127.1米
【解析】分析:(1)过P作PF⊥BD于F,作PE⊥AB于E,设PF=5x,在Rt△ABC中求出AB,用含x的式子表示出AE,EP,由tan∠APE,求得x即可;(2)在Rt△CPF中,求出CP的长.
详解:过P作PF⊥BD于F,作PE⊥AB于E,
∵斜坡的坡度i=5:12,
设PF=5x,CF=12x,
∵四边形BFPE为矩形,
∴BF=PEPF=BE.
在RT△ABC中,BC=90,
tan∠ACB=![]() ,
,
∴AB=tan63.4°×BC≈2×90=180,
∴AE=AB-BE=AB-PF=180-5x,
EP=BC+CF≈90+120x.
在RT△AEP中,
tan∠APE=![]() ,
,
∴x=![]() ,
,
∴PF=5x=![]() .
.
答:此人所在P的铅直高度约为14.3米.
由(1)得CP=13x,
∴CP=13×![]() 37.1,BC+CP=90+37.1=127.1.
37.1,BC+CP=90+37.1=127.1.
答:从P到点B的路程约为127.1米.

练习册系列答案
相关题目