Question

【题目】如图，点，，在同一直线上，射线在的内部，，分别是，的平分线，请探究与的数量关系.

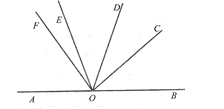
（1）当，时，求出和的度数，并写出他们的数量关系；

（2）一般情况下，写出和之间的数量关系，并说明理由.

Answer 1

【答案】（1）=30°，=15°，∠COD=2；（2）∠COD=2，理由见解析.

【解析】

（1）根据平角的定义和已知条件求出∠AOD、∠AOC和∠COD，然后根据角平分线的定义求出∠EOA和∠FOA，从而求出，即可得出和之间的数量关系；

（2）设，，同理即可求出和与的关系，即可得出和之间的数量关系.

解：（1）∵，

∴∠AOD=180°－，∠AOC=180°－，∠COD=

∵，分别是，的平分线

∴∠EOA=，∠FOA=

∴=∠EOA－∠FOA=15°

∴∠COD=2；

（2）∠COD=2，理由如下：

设，

∴∠AOD=180°－，∠AOC=180°－，∠COD=

∵，分别是，的平分线

∴∠EOA=，∠FOA=

∴=∠EOA－∠FOA=

∴∠COD=2；