Question

【题目】若0°＜α＜90°，那么，以sinα、cosα、tanα·cotα为三边的△ABC的内切圆半径与外接圆半径之和是（ ）

A.2B.C.D.

Answer 1

【答案】C

【解析】

先根据三角形的三边关系判断出△ABC的形状，再根据切线长定理即可求出其内切圆的半径，由圆周角定理即可求出外接圆的半径．

解：∵tanαcotα=1=sin2α+cos2α，
∴△ABC是直角三角形，
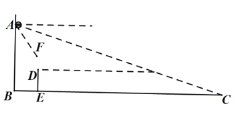
如图所示，设△ABC内切圆的半径r，外接圆的半径为R，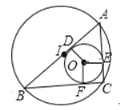

∵AD=AE，CE=CF，BD=BF，

易得四边形OECF为正方形，∴CE=CF=r，

∴AB=AD+BD=AE+BF=AC-CE+BC-CF=sinα+cosα-2r=1，
∴r=．

∵∠ACB=90°，∴AB为△ABC外接圆的直径，
∴R=，

∴r+R=，

故选：C．