题目内容
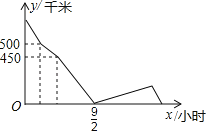
【题目】甲、乙两人驾车分别从A、B两地相向而行，乙出发半小时后甲出发，甲出发1.5小时后汽车出现故障，于是甲停下修车，半小时后甲修好后继续沿原路按原速与乙相遇，相遇后甲随即调头以原速返回A地，乙也继续向A地行驶，甲、乙两车之间的距离（y/千米）与甲驾车时间x（小时）之间的关系如图所示，当乙到达A地时，甲距离B地_____千米．
【答案】756
【解析】
利用速度＝路程÷时间可求出乙的速度及甲、乙的速度和，二者做差后可得出甲的速度，由甲出发的时间结合修车所需时间，可求出两人相遇后乙行驶到A地所需时间，根据“路程、速度与时间的关系”可求出结论．
解：乙的速度为（500﹣450）÷
＝100（千米/时），
甲、乙的速度和为450÷（
﹣2）＝180（千米/时），
甲的速度为：180﹣100＝80（千米/时），
两人相遇后，甲返回A地所需时间为：-=4（小时），
故相遇地点距离A地为：80×4＝320（千米），
乙从相遇地点到达A地需要行驶的时间为：320÷100＝3.2（小时），
当乙到达A地时，甲距离B地：5×100+80×3.2＝756（千米）．
故答案为：756．
练习册系列答案
相关题目
