题目内容
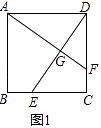
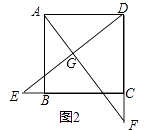
【题目】在菱形ABCD中,P是AB上一动点(但不与A、B两点重合),DP的延长线交CB延长线于点E.
(1)△APD与△BPE是否总相似,为什么?
(2)当P为AB中点时,求证:点B是EC中点.
(3)当PD⊥AB时,设AD=10,sinA=![]() ,求BE的长.
,求BE的长.

【答案】(1)相似.理由见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)由四边形ABCD为菱形,得到AD∥BC,即可得到结论;(2)先由角角边证得△APD≌△BPE,AD=BE,再由四边形ABCD为菱形, 得到AD=BC,即BE=BC,即点B为EC中点.(3)再Rt△APD中,由AD=10,sinA=![]() 得PD=8,AP=6,故PB=4,由△APD∽△BPE可得
得PD=8,AP=6,故PB=4,由△APD∽△BPE可得![]() =
=![]() ,即可求得BE长.
,即可求得BE长.
试题解析:: (1)相似.
∵四边形ABCD为菱形,
∴AD∥BC.
∴∠DAP=∠EBP,∠ADP=∠BEP.
∴△APD△BPE.
(2)∵P是AB中点,
∴AP=BP.
又∵∠DAP=∠EBP,∠ADP=∠BEP,
∴△APD≌△BPE.
∴AD=BE.
∵四边形ABCD为菱形,
∴AD=BC.
∴BE=BC.
即点B为EC中点.
(3)∵PD⊥AB,AD=10,sinA=![]() . ∴PD=8.∴AP=6.∴PB=AB—AP=10—6=4.
. ∴PD=8.∴AP=6.∴PB=AB—AP=10—6=4.
∵△APD∽△BPE,∴ ![]() =
=![]() ∴BE=
∴BE=![]() =
=![]() =
=![]()

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目