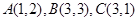题目内容
如果一个矩形对折后和原矩形相似,则对折后矩形长边与短边的比为 ( )
| A.4:1 | B.2:1 | C.1.5:1 | D. :1 :1 |
D
根据相似多边形对应边的比相等,设出原来矩形的长与宽,就可得到一个方程,解方程即可求得.

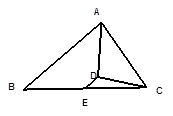
解:根据条件可知:矩形AEFB∽矩形ABCD.
∴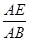 =
= .
.
设AD=x,AB=y,则AE=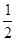 x.则
x.则 =
=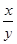 ,即:
,即: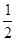
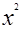 =
= .
.
∴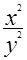 =2.
=2.
∴x:y=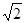 :1.即原矩形长与宽的比为
:1.即原矩形长与宽的比为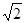 :1.
:1.
∵矩形AEFB∽矩形ABCD,
∴对折后矩形长边与短边的比为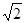 :1.
:1.
故选D.
点根据相似形的对应边的比相等,把几何问题转化为方程问题,正确分清对应边,以及正确解方程是解决本题的关键.

解:根据条件可知:矩形AEFB∽矩形ABCD.
∴
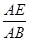 =
= .
.设AD=x,AB=y,则AE=
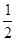 x.则
x.则 =
=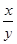 ,即:
,即: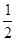
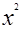 =
= .
.∴
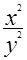 =2.
=2.∴x:y=
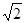 :1.即原矩形长与宽的比为
:1.即原矩形长与宽的比为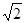 :1.
:1.∵矩形AEFB∽矩形ABCD,
∴对折后矩形长边与短边的比为
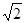 :1.
:1.故选D.
点根据相似形的对应边的比相等,把几何问题转化为方程问题,正确分清对应边,以及正确解方程是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
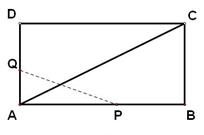
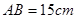 ,
,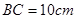 ,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动。如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与
,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动。如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与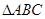 相似?
相似?