题目内容
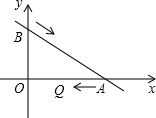 如图,在直角坐标平面内,点0为坐标原点,直线AB经过A(8,0),B(0,6),现有两个动点P,Q.动点P从B沿BA方向以1个单位每秒的速度向A运动,动点Q从A沿AO方向2个单位每秒的速度向O运动,当P,Q两点中的任何一点到达终点时,运动停止.
如图,在直角坐标平面内,点0为坐标原点,直线AB经过A(8,0),B(0,6),现有两个动点P,Q.动点P从B沿BA方向以1个单位每秒的速度向A运动,动点Q从A沿AO方向2个单位每秒的速度向O运动,当P,Q两点中的任何一点到达终点时,运动停止.(1)求直线AB的解析式.
(2)问当运动时间t为多少秒时,以A、P、Q为顶点的三角形为直角三角形.
分析:(1)根据已知条件,把A、B两点的坐标代入y=kx+b,即可求出k、b的值,很容易地就得到了直线AB的解析式;
(2)本小题要进行讨论,首先当A为直角顶点时,不符合题意,所以A不为直角顶点;当P为直角顶点时,求三角形相似,根据其性质,即可得t的值;当O为直角顶点时,同样求证三角形相似,根据其性质,即可得t的值.
(2)本小题要进行讨论,首先当A为直角顶点时,不符合题意,所以A不为直角顶点;当P为直角顶点时,求三角形相似,根据其性质,即可得t的值;当O为直角顶点时,同样求证三角形相似,根据其性质,即可得t的值.
解答:解:(1)设AB解析式为y=kx+6,过A(8,0),则k=-
,∴解析式为y=-
x+6(2分)
(2)∵Q在OA上,∴∠PAQ≠90°,在Rt△ABO中,AB=10,(1分)
∴①当PQ⊥AQ时,△APQ为直角三角形.易得△APQ∽△ABO,则
=
即
=
,
∴t=
(2分)
②当PQ⊥AP时,△APQ为直角三角形.易得△APQ∽△AOB,则
=
即
=
,
∴t=
(2分)
综上所得,当t=
或t=
时,△APQ为直角三角形.
| 3 |
| 4 |
| 3 |
| 4 |
(2)∵Q在OA上,∴∠PAQ≠90°,在Rt△ABO中,AB=10,(1分)
∴①当PQ⊥AQ时,△APQ为直角三角形.易得△APQ∽△ABO,则
| AP |
| AB |
| AQ |
| AO |
| 10-t |
| 10 |
| 2t |
| 8 |
∴t=
| 20 |
| 7 |
②当PQ⊥AP时,△APQ为直角三角形.易得△APQ∽△AOB,则
| AP |
| AO |
| AQ |
| AB |
| 10-t |
| 8 |
| 2t |
| 10 |
∴t=
| 50 |
| 13 |
综上所得,当t=
| 20 |
| 7 |
| 50 |
| 13 |
点评:本题主要考查根据点的坐标求直线的解析式、相似三角形的判定和性质等知识点,关键在于根据题意和图形,正确分析确定哪些点可以为△APQ为直角三角形直角顶点,并逐一讨论求证.

练习册系列答案
相关题目
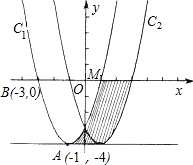 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)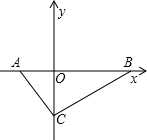 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC= 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是