ЬтФПФкШн
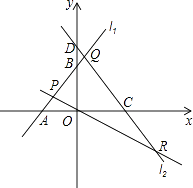
ЁОЬтФПЁПШчЭМ,вбжЊвЛДЮКЏЪ§y=0.5x+1ЕФЭМЯѓгыxжсНЛгкЕуA,гыyжсНЛгкЕуB,ЖўДЮКЏЪ§y=0.5x2+bx+cЕФЭМЯѓгывЛДЮКЏЪ§y=0.5x+1ЕФЭМЯѓНЛгкЕуBЁЂCСНЕу,гыxжсНЛгкDЁЂEСНЕу,ЧвDЕузјБъЮЊЃЈ1,0ЃЉЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкдкxжсЩЯгавЛЖЏЕуPЃЌДгOЕуГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШбиxжсЯђгвдЫЖЏЃЌЪЧЗёДцдкЖЏЕуPЃЌЪЙЕУЁїPBCЪЧвдPЮЊжБНЧЖЅЕуЕФжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуPдЫЖЏЪБМфtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЖЏЕуPдкxжсЩЯЃЌЖЏЕуQдкЩфЯпACЩЯЃЌЭЌЪБДгAЕуГіЗЂЃЌЕуPбиxжсе§ЗНЯђвдУПУы2ИіЕЅЮЛЕФЫйЖШдЫЖЏЃЌЕуQвдУПУыaИіЕЅЮЛЕФЫйЖШбиЩфЯпACдЫЖЏЃЌЪЧЗёДцдквдAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABDЯрЫЦЃПШєДцдкЃЌЧѓaЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉНтЮіЪНЮЊЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉt=1Лђ3ЃЛ
ЃЈ3ЃЉЕБaжЕЮЊ![]() Лђ
Лђ![]() ЪБ,ЁїAPQгыЁїABDЯрЫЦ
ЪБ,ЁїAPQгыЁїABDЯрЫЦ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнвЛДЮКЏЪ§ЕФНтЮіЪНПЩевГіЕуBЕФзјБъЃЌдйИљОнЕуAЁЂDЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛЃЈ2ЃЉМйЩшДцдкЃЌдђЕуPЕФзјБъЮЊЃЈtЃЌ0ЃЉЃЎСЊСЂжБЯпгыХзЮяЯпНтЮіЪНГЩЗНГЬзщЃЌНтЗНГЬзщЧѓГіЕуCЕФзјБъЃЌИљОнЕуBЁЂPЕФзјБъРћгУСНЕуМфЕФОрРыЙЋЪНМДПЩЧѓГіPBЁЂPCЁЂBCЕФГЄЖШЃЌдйРћгУЙДЙЩЖЈРэМДПЩЕУГіЙигкtЕФвЛдЊЖўДЮЗНГЬЃЌНтЗНГЬМДПЩЕУГіНсТлЃЛЃЈ3ЃЉМйЩшДцдкЃЌдђAP=2tЃЌAQ=atЃЎгЩвЛДЮКЏЪ§НтЮіЪНМДПЩевГіЕуAЕФзјБъЃЌНсКЯЕуBЁЂDЕФзјБъМДПЩЕУГіABЁЂADЕФГЄЖШЃЌЗжЁїPAQЁзBADКЭЁїPAQЁзЁїDABСНжжЧщПіПМТЧЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪМДПЩЕУГіЙигкaЕФвЛдЊвЛДЮЗНГЬЃЌНтЗНГЬМДПЩЧѓГіaжЕЃЌДЫЬтЕУНтЃЎ
ЪдЬтНтЮіЃК(1)НЋB(0,1),D(1,0)ЕФзјБъДњШыy=![]() x2+bx+cЃЌ
x2+bx+cЃЌ
ЕУЃК 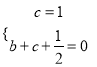 ЃЌ
ЃЌ
НтЕУЃК 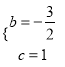 ЃЌ
ЃЌ
ЙЪНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
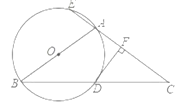
(2)ЩшЗћКЯЬѕМўЕФЕуPДцдк,СюP(a,0):
ЕБPЮЊжБНЧЖЅЕуЪБЃЌШчЭМЃКЙ§CзїCFЁЭxжсгкFЃЛ
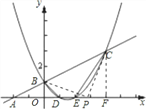
ЁпRtЁїBOPЁзRtЁїPCFЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
ећРэЕУa24a+3=0ЃЌ
НтЕУa=1Лђa=3ЃЛ
ЙЪПЩЕУt=1Лђ3.
(3)ДцдкЗћКЯЬѕМўЕФtжЕЃЌЪЙЁїAPQгыЁїABDЯрЫЦЃЌ
ЂйЕБЁїAPQЁзЁїABDЪБ, ![]() ЃЌ
ЃЌ
НтЕУЃКa=![]() ЃЛ
ЃЛ
ЂкЕБЁїAPQЁзЁїADBЪБ, ![]() ЃЌ
ЃЌ
НтЕУЃКa=![]() ЃЌ
ЃЌ
ЁрДцдкЗћКЯЬѕМўЕФaжЕ,ЪЙЁїAPQгыЁїABDЯрЫЦ,a=![]() Лђ
Лђ![]() .
.