题目内容
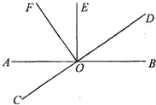
【题目】如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
(1)图中∠AOF的余角有 ;(把符合条件的角都填出来)
(2)如果∠AOD=140°,那么根据 ,可得∠BOC= 度;
(3)已知5∠EOF=∠AOD,求∠EOF的度数.
【答案】(1)∠EOF,∠AOC,∠BOD; (2)对顶角相等,140;(3)∠EOF=30°.
【解析】
(1)根据余角的定义、性质,可得答案;
(2)根据对顶角的性质,可得答案;
(3)根据余角的性质,可得∠EOF与∠BOD的关系,根据平角的定义,可得答案.
解:(1)图中∠AOF的余角有∠EOF,∠AOC,∠BOD;
(2)如果∠AOD=140°,那么根据 对顶角相等,可得∠BOC=140°;
故答案为:对顶角相等,140;
(3)∵∠EOF+AOF=90°,∠AOC+∠AOF=90°,∴∠EOF=∠AOC=∠BOD.
∵∠AOD+∠BOD=180°,5∠EOF=∠AOD∴5∠EOF+∠BOD=180°,即6∠EOF=180°,∠EOF=30°.

练习册系列答案
相关题目


