题目内容
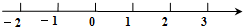 (1)已知:(x+1)2=16,求x
(1)已知:(x+1)2=16,求x
(2)计算: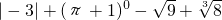
(3)解不等式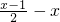 ≥-2,并把解集在数轴上表示出来.
≥-2,并把解集在数轴上表示出来.
(4)解不等式组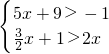 ,并写出范围内的正整数解.
,并写出范围内的正整数解.
解:(1)∵(x+1)2=16,
∴x+1=±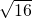 ,
,
∴x=-1±4,
∴x1=-5,x2=3;
(2)原式=3+1-3+2
=3;
(3)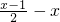 ≥-2,
≥-2,
去分母得,x-1-2x≥-4,
移项、合并同类项得,-x≥3,
系数化为1得,x≤-3;
在数轴上表示为:
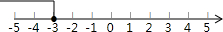
(4)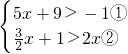 ,由①得,x>-2,由②得,x<2,
,由①得,x>-2,由②得,x<2,
故此不等式组的解集为:-2<x<2,
故x的正整数解为:1.
分析:(1)由于方程左边是一个完全平方式,故可用直接开方法求出x的值;
(2)根据实数混合运算的法则进行计算即可;
(3)先根据不等式的基本性质求出不等式的解集,再把其解集在数轴上表示出来即可;
(4)分别求出各不等式的解集,再求出其公共解集,并找出符合条件的x的正整数解即可.
点评:本题考查的是解一元二次方程、解一元一次不等式及解一元一次不等式组,涉及面较广,但比较简单.
∴x+1=±
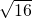 ,
,∴x=-1±4,
∴x1=-5,x2=3;
(2)原式=3+1-3+2
=3;
(3)
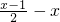 ≥-2,
≥-2,去分母得,x-1-2x≥-4,
移项、合并同类项得,-x≥3,
系数化为1得,x≤-3;
在数轴上表示为:
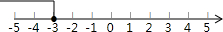
(4)
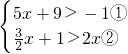 ,由①得,x>-2,由②得,x<2,
,由①得,x>-2,由②得,x<2,故此不等式组的解集为:-2<x<2,
故x的正整数解为:1.
分析:(1)由于方程左边是一个完全平方式,故可用直接开方法求出x的值;
(2)根据实数混合运算的法则进行计算即可;
(3)先根据不等式的基本性质求出不等式的解集,再把其解集在数轴上表示出来即可;
(4)分别求出各不等式的解集,再求出其公共解集,并找出符合条件的x的正整数解即可.
点评:本题考查的是解一元二次方程、解一元一次不等式及解一元一次不等式组,涉及面较广,但比较简单.

练习册系列答案
相关题目
 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定. 如图,已知矩形ABCD,OA与x轴正半轴夹角为60°,点A的横坐标为2,点C的横坐标为
如图,已知矩形ABCD,OA与x轴正半轴夹角为60°,点A的横坐标为2,点C的横坐标为