Question

如图，点A、B、D、在⊙O上，弦AE、BD的延长线相交于点C.。若AB是⊙O的直径，D是BC的中点.

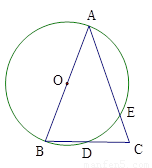
（1）试判断AB、AC之间的大小关系，并给出证明；

（2）在上述题设条件下，△ABC还需满足什么条件，点E才一定是AC的中点？（直接写出结论）

 

Answer 1

【答案】

（1）AB=AC；（2）△ABC为正三角形，或AB=BC，或AC=BC，或∠A=∠B，或∠A=∠C．

【解析】

试题分析：（1）连接AD；由圆周角定理可得AD⊥BC，又D是BC的中点，因此AD是BC的垂直平分线，由此可得出AB=AC的结论．

（2）若E是AC的中点，那么连接BE后，同（1）可证得AB=BC；由（1）知：AB=AC，那么此时AB=AC=BC，即△ABC是等边三角形．可根据这个结论来添加条件．

（1）AB=AC．

证法一：

连接AD．

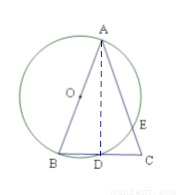
∵AB是⊙O的直径，

∴AD⊥BC．

∵AD为公共边，BD=DC，

∴Rt△ABD≌Rt△ACD（SAS）．∴AB=AC．

证法二：

连接AD．

∵AB是⊙O的直径，

∴AD⊥BC．

又BD=DC，∴AD是线段BD的中垂线．

∴AB=AC．

（2）△ABC为正三角形，或AB=BC，或AC=BC，或∠A=∠B，或∠A=∠C．

考点：本题考查了圆周角定理、全等三角形的判定和性质、等腰三角形的性质、等边三角形的判定

点评：解答本题的关键数是掌握好直径所对的圆周角是直角，垂直平分线上的点到线段两端的距离相等。