题目内容
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|
分析:过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.设出C点坐标,利利用勾股定理求出AC,OC长,再求C点坐标,即可得到答案.
解答: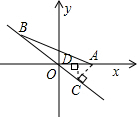 解:过A作AC⊥BO,过C作CD⊥OA,当B运动到C处时,线段AB最短,
解:过A作AC⊥BO,过C作CD⊥OA,当B运动到C处时,线段AB最短,
∵C在直线y=-x上,
∴AC=OC,
设C点坐标为(m,-m),
在Rt△ACO中,AC2+CO2=AO2,
∴AC2+CO2=(2
)2,
∴AC=OC=2,
∵CD⊥OA,
∴CD垂直平分OA,
∴AD=OD=
AO=
,
∴m=
,-m=-
,
∴C(
,-
).
故选D.
 解:过A作AC⊥BO,过C作CD⊥OA,当B运动到C处时,线段AB最短,
解:过A作AC⊥BO,过C作CD⊥OA,当B运动到C处时,线段AB最短,∵C在直线y=-x上,
∴AC=OC,
设C点坐标为(m,-m),
在Rt△ACO中,AC2+CO2=AO2,
∴AC2+CO2=(2
| 2 |
∴AC=OC=2,
∵CD⊥OA,
∴CD垂直平分OA,
∴AD=OD=
| 1 |
| 2 |
| 2 |
∴m=
| 2 |
| 2 |
∴C(
| 2 |
| 2 |
故选D.
点评:此题主要考查了垂线段最短,勾股定理,一次函数的综合运用,题目综合性较强,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2, 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧. 如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 如图,点A的坐标为( )
如图,点A的坐标为( )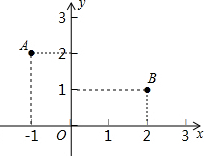 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )