题目内容
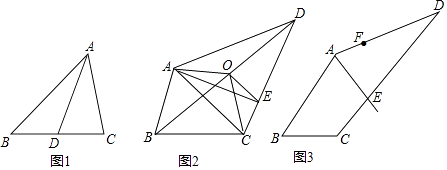
【题目】如图,已知FD⊥BC于D,DE⊥AB于E,∠B=∠C,∠AFD=140°,求∠EDF的度数. 
【答案】解:∵FD⊥BC,DE⊥AB,
∴∠BED=∠FDC=90°,
∴∠B+∠BDE=90°,∠C+∠CFD=90°,
∵∠B=∠C,
∴∠BDE=∠CFD=180°﹣∠AFD=180°﹣140°=40°,
∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣40°﹣90°=50°.
【解析】根据垂直定义求出∠BED=∠FDC=90°,根据三角形内角和定理求出∠BDE=∠CFD=180°﹣∠AFD=40°,代入∠EDF=180°﹣∠BDE﹣∠FDC求出即可.
【考点精析】根据题目的已知条件,利用三角形的内角和外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目