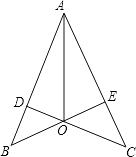
题目内容
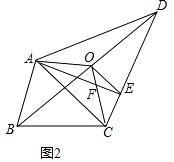
【题目】我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:在四边形ABCD(图2)中,取对角线BD的中点O,连接OA、OC.得折线AOC,再过点O作OE∥AC交CD于E,则直线AE即为四边形ABCD的一条“好线”.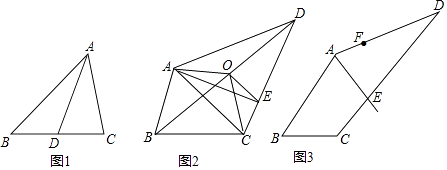
(1)如图(1),试说明中线AD平分△ABC的面积;
(2)如图(2),请你探究四边形ABCO的面积和四边形ABCD面积的关系,并说明理由;
(3)解:在图(2)中,请你说明直线AE是四边形ABCD的一条“好线”;
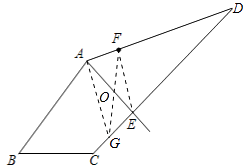
(4)如图(3),若AE为一条“好线”,F为AD边上的一点,请作出四边形ABCD经过F点的“好线”,并对你的画图作适当说明.
【答案】
(1)
解:如图1中,作AH⊥BC于H.
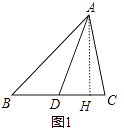
∵AD是中线,
∴BD=CD,
∴S△ABD= ![]() BDAH,S△ADC=
BDAH,S△ADC= ![]() DCAH,
DCAH,
∴S△ABD=S△ADC,
∴中线AD平分△ABC的面积.
(2)
解:结论:S四边形ABCO= ![]() S四边形ABCD.
S四边形ABCD.
如图2中,
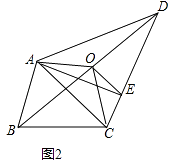
理由:由(1)知,S△AOB=S△AOD,S△BOC=S△DOC,
∴ ![]()
∴S四边形ABCO= ![]() S四边形ABCD.
S四边形ABCD.
(3)
如图2中,设AE交OC于F.
∵OE∥AC,
∴S△AOE=S△COE,
∴S△AOF=S△CEF,
又因为(2)知,折线AOC能平分四边形ABCD的面积,
∴直线AE平分四边形ABCD的面积,即AE是四边形ABCD的一条“好线”.
(4)
解:连接EF,过A作EF的平行线交CD于点G,连接FG,则GF为一条“好线”.
∵AG∥EF,
∴S△AGE=S△AFG.
设AE与FG的交点是O.则S△AOF=S△GOE,
又AE为一条“好线”,所以GF为一条“好线”.
【解析】(1)如图1中,作AH⊥BC于H.由S△ABD= ![]() BDAH,S△ADC=
BDAH,S△ADC= ![]() DCAH,因为BD=CD,所以S△ABD=S△ADC;(2)利用(1)中结论可以证明S四边形ABCO=
DCAH,因为BD=CD,所以S△ABD=S△ADC;(2)利用(1)中结论可以证明S四边形ABCO= ![]() S四边形ABCD;(3)设AE交OC于F.由OE∥AC,推出S△AOE=S△COE , 推出S△AOF=S△CEF , 又因为(2)知,折线AOC能平分四边形ABCD的面积,即可推出直线AE平分四边形ABCD的面积;(4)连接EF,过A作EF的平行线交CD于点G,连接FG,则GF为一条“好线”.由AG∥EF,推出S△AGE=S△AFG . 设AE与FG的交点是O.则S△AOF=S△GOE , 又AE为一条“好线”,所以GF为一条“好线”;
S四边形ABCD;(3)设AE交OC于F.由OE∥AC,推出S△AOE=S△COE , 推出S△AOF=S△CEF , 又因为(2)知,折线AOC能平分四边形ABCD的面积,即可推出直线AE平分四边形ABCD的面积;(4)连接EF,过A作EF的平行线交CD于点G,连接FG,则GF为一条“好线”.由AG∥EF,推出S△AGE=S△AFG . 设AE与FG的交点是O.则S△AOF=S△GOE , 又AE为一条“好线”,所以GF为一条“好线”;