Question

【题目】如图，AB是⊙O的弦，AB=2，点C在上运动，且∠ACB=30°.

（1）求⊙O的半径；

（2）设点C到直线AB的距离为x，图中阴影部分的面积为y，求y与x之间的函数关系，并写出自变量x的取值范围．

Answer 1

【答案】（1）的半径是2；（2）.

【解析】试题分析：（1）根据圆周角定理得到△AOB是等边三角形，求出 O的半径；（2）根据图形可得阴影部分面积为三角形ABP的面积+弓形AB的面积，用含有x的代数式表示阴影部分的面积即可，注意x的取值范围.

试题解析：（1）∵∠APB=30°，

∴∠AOB=60°，

∵AO=BO，

∴△AOB是等边三角形，

∵AB=2，

∴OA=OB=2，

∴☉O的半径为2；

（2）过O作OD⊥AB交AB于点C.

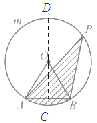
∵OA=OB ，OD⊥AB， AB=2，

∴AC=CB=1，

∴OC=，

∴S△ABP=·AB·x=x，

S阴影= ·AB·OC+x，

计算得S阴影=+x，

结合已知可得当x取最大值时，P点的位置在点D处.

此时CD=CO+OP=2+.

那么x的取值范围是0≤x＜2+，

所以y= x+(0≤x＜2+).