题目内容
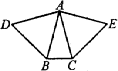
如图所示，已知等腰三角形ABC的底边BC=20cm，D是腰AB上一点，且CD=16cm，BD=12cm，求△ABC的周长．分析：先判断CD⊥AB，在Rt△ACD中，利用勾股定理求出x，得出AC，继而可得出△ABC的周长．
解答：解：在△BCD中，BC=20cm，CD=16cm，BD=12cm，
∵BD2+DC2=BC2，
∴△BCD中是直角三角形，∠BDC=90°，BD⊥DC，
设AD=x，则AC=x+12，
在Rt△ADC中，∵AC2=AD2+DC2，
∴x2+162=（x+12）2，
解得：x=
．
∴△ABC的周长为：（
+12）×2+20=
cm．
∵BD2+DC2=BC2，
∴△BCD中是直角三角形，∠BDC=90°，BD⊥DC，
设AD=x，则AC=x+12，
在Rt△ADC中，∵AC2=AD2+DC2，
∴x2+162=（x+12）2，
解得：x=
| 14 |
| 3 |
∴△ABC的周长为：（
| 14 |
| 3 |
| 160 |
| 3 |
点评：本题考查了勾股定理的知识，解答本题的关键是利用勾股定理求出AD的长度，得出腰的长度，难度一般．
练习册系列答案
相关题目
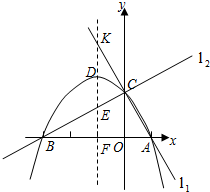已知两直线l1，l2分别经过点A（1，0），点B（-3，0），并且当两直线同时相交于y正半轴的点C时，恰好有l1⊥l2，经过点A、B、C的抛物线的对称轴与直线l1交于点K，如图所示．
