题目内容
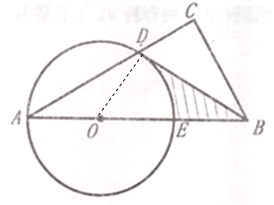
【题目】如图．在⊙O中. AE直径，AD是弦，B为AE延长线上--点，作BC⊥AD，与AD延长线交于点C．且∠CBD=∠A．
(1)判断直线BD与⊙0的位置关系，并证明你的结论；
(2)若∠A=30
，OA=6，求图中阴影部分的面积.
【答案】（1）见解析；（2）
【解析】试题分析：（1）连结OD，证明∠ODB=90°即可；
（2）根据阴影面积=△BOD的面积－扇形DOE的面积计算即可．
试题解析：解：（1）直线BD与⊙O相切． 证明如下：
连接OD．∵OA＝OD，∴∠ODA＝∠A．又∵∠CBD＝∠A ，∴∠CBD＝∠ODA ．
∵BC⊥AD，∴∠C＝90°，∴∠CBD＋∠CDB＝90°，∴∠ODA＋∠CDB＝90°，∴∠ODB＝90°， ∴BD⊥OD．又∵OD是半径，∴BD是⊙O的切线 ；
（2）∵∠A＝30°，∴∠DOB＝60°．
∵OA＝6，∴OD＝6．又由（1），知∠ODB＝90°，∴BO＝12，∴BD＝
，
．
练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表，
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论：
（1）二次函数y=ax2+bx+c 有最小值，最小值为-3；
（2）抛物线与y轴交点为（0，-3）；
（3）二次函数y=ax2+bx+c 的图像对称轴是x=1；
（4）本题条件下，一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是（ ）
A. 4 B. 3 C. 2 D. 1
