题目内容
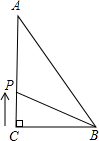 如图,Rt△ABC中,∠ACB=Rt∠,BC=6cm,AC=8cm,动点P从C点出发以1cm/秒的速度沿CA,AB运动到B.
如图,Rt△ABC中,∠ACB=Rt∠,BC=6cm,AC=8cm,动点P从C点出发以1cm/秒的速度沿CA,AB运动到B.
(1)设P点运动的路程为xcm,△BCP的面积为ycm2,求y与x之间的函数关系式.
(2)从C点出发几秒钟时,△BCP的面积为△ABC的 ?
?
解:(1)①P点在AC上,
∴PC=x,
∵∠ACB=90°,BC=6cm,
∵△BCP的面积为ycm2,
∴y=BC•x• ,即y=3x;
,即y=3x;
②P点在AB上,
∵∠ACB=90°,BC=6cm,AC=8cm,
∴AB=10,
∴BP=10-x,
作CD⊥AB,
∴△ABC∽△CBD,
∴AC:CD=AB:BC,
∴CD=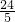 ,
,
∵△BCP的面积为ycm2,
∴y=(10-x)•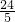
 ,
,
∴y=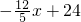 .
.
(2)∵BC=6cm,AC=8cm,
∴△ABC的面积=24cm2,
∴△BCP的面积为:24• =6,
=6,
①P点在AB上,
∴6=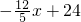 ,
,
∴x=7.5cm,
∵点P从C点出发的速度为1cm/秒,
∴7.5cm÷1cm/秒=7.5秒,
∴从C点出发7.5秒钟时,△BCP的面积为△ABC的 .
.
②P点在AC上,
∴6=3x,
∴x=2,
∵点P从C点出发的速度为1cm/秒,
∴2cm÷1cm/秒=2秒,
∴从C点出发2秒钟时,△BCP的面积为△ABC的 .
.
答:从C点出发2秒或7.5秒钟时,△BCP的面积为△ABC的 .
.
分析:(1)首先根据情况进行讨论,第一种情况:P点在AC上,那么y=BC•x• ,即y=3x;第二种情况:P点在AB上,那么根据勾股定理求出AB=10,然后作出BP的高,通过求证三角形相似,求出高的值,即可推出函数式.
,即y=3x;第二种情况:P点在AB上,那么根据勾股定理求出AB=10,然后作出BP的高,通过求证三角形相似,求出高的值,即可推出函数式.
(2)首先求出△ABC的面积,即可确定△BCP的面积,然后根据(1)的结论,即可推出路程x的值,再根据P点的运动速度,便可求出运动时间.
点评:本题主要考查相似三角形的判定和性质、勾股定理,关键在于分情况进行讨论,求出y关于x的解析式.
∴PC=x,
∵∠ACB=90°,BC=6cm,
∵△BCP的面积为ycm2,
∴y=BC•x•
 ,即y=3x;
,即y=3x;②P点在AB上,
∵∠ACB=90°,BC=6cm,AC=8cm,

∴AB=10,
∴BP=10-x,
作CD⊥AB,
∴△ABC∽△CBD,
∴AC:CD=AB:BC,
∴CD=
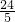 ,
,∵△BCP的面积为ycm2,
∴y=(10-x)•
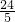
 ,
,∴y=
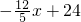 .
.(2)∵BC=6cm,AC=8cm,
∴△ABC的面积=24cm2,
∴△BCP的面积为:24•
 =6,
=6,①P点在AB上,
∴6=
 ,
,∴x=7.5cm,
∵点P从C点出发的速度为1cm/秒,
∴7.5cm÷1cm/秒=7.5秒,
∴从C点出发7.5秒钟时,△BCP的面积为△ABC的
 .
.②P点在AC上,
∴6=3x,
∴x=2,
∵点P从C点出发的速度为1cm/秒,
∴2cm÷1cm/秒=2秒,
∴从C点出发2秒钟时,△BCP的面积为△ABC的
 .
.答:从C点出发2秒或7.5秒钟时,△BCP的面积为△ABC的
 .
.分析:(1)首先根据情况进行讨论,第一种情况:P点在AC上,那么y=BC•x•
 ,即y=3x;第二种情况:P点在AB上,那么根据勾股定理求出AB=10,然后作出BP的高,通过求证三角形相似,求出高的值,即可推出函数式.
,即y=3x;第二种情况:P点在AB上,那么根据勾股定理求出AB=10,然后作出BP的高,通过求证三角形相似,求出高的值,即可推出函数式.(2)首先求出△ABC的面积,即可确定△BCP的面积,然后根据(1)的结论,即可推出路程x的值,再根据P点的运动速度,便可求出运动时间.
点评:本题主要考查相似三角形的判定和性质、勾股定理,关键在于分情况进行讨论,求出y关于x的解析式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

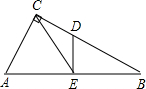 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB=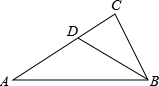 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )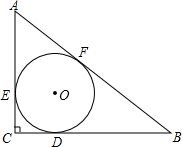 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.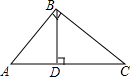 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.