题目内容
附加题:
观察下列等式: ,
, ,
, ,
,
将以上三个等式两边分别相加得:
 .
.
(1)直接写出下列各式的计算结果:
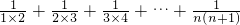 =______
=______
(2)猜想并写出: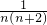 =
= (
( -
- ).
).
(3)探究并解方程: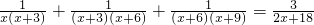 .
.
解:因为(1) ,
,
 ,
,
 ,
,
…
 =
= -
- ,
,
所以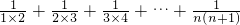 ,
,
=1- +
+ -
- +
+ -
- +…+
+…+ -
- ,
,
=1- ,
,
= ;
;
(2)因为 -
-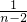 =
=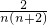 ,
,
所以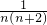 =
= (
( -
- );
);
(3)类比(2)的结论,可以得到,
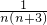 =
= (
( -
-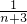 ),
),
所以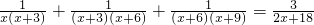 ,
,
 (
( -
-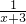 +
+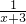 -
-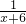 +
+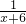 -
-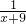 )=
)=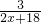 ,
,
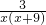 =
=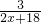 ,
,
解得x1=-9,x2=2,
经检验,x1=-9是增根,x2=2是原方程的根.
分析:(1)由等式: ,
, ,
, ,两边分别相加得:
,两边分别相加得:
 ,类比上面的做法得到答案;
,类比上面的做法得到答案;
(2)因 -
-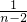 =
=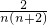 ,再由
,再由 -
- =
= 猜想出结论;
猜想出结论;
(3)由(2)的结论,可以推出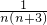 =
= (
( -
-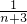 ),进一步解出方程.
),进一步解出方程.
点评:解决此类问题,从特殊中找出一般情况,利用类比的思想进一步解决问题.
 ,
, ,
, ,
,…
 =
= -
- ,
,所以
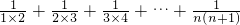 ,
,=1-
 +
+ -
- +
+ -
- +…+
+…+ -
- ,
,=1-
 ,
,=
 ;
;(2)因为
 -
-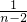 =
=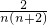 ,
,所以
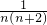 =
= (
( -
- );
);(3)类比(2)的结论,可以得到,
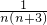 =
= (
( -
-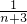 ),
),所以
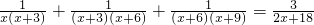 ,
, (
( -
-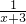 +
+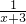 -
-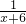 +
+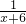 -
-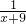 )=
)=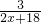 ,
,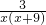 =
=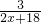 ,
,解得x1=-9,x2=2,
经检验,x1=-9是增根,x2=2是原方程的根.
分析:(1)由等式:
 ,
, ,
, ,两边分别相加得:
,两边分别相加得: ,类比上面的做法得到答案;
,类比上面的做法得到答案;(2)因
 -
-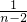 =
=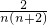 ,再由
,再由 -
- =
= 猜想出结论;
猜想出结论;(3)由(2)的结论,可以推出
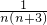 =
= (
( -
- ),进一步解出方程.
),进一步解出方程.点评:解决此类问题,从特殊中找出一般情况,利用类比的思想进一步解决问题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 附加题:
附加题: