题目内容
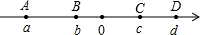 附加题:
附加题:(1)已知|a-2|+|b+6|=0,则a+b=
-4
-4
.(2)观察下列等式:
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
①猜想并写出:
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+1 |
②直接写出结果:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2006×2007 |
| 2006 |
| 2007 |
| 2006 |
| 2007 |
(3)在数轴上有两点,它们到原点的距离分别是2和3,问这两点之间的距离是多少?
(4)求|
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 99 |
| 1 |
| 98 |
| 1 |
| 100 |
| 1 |
| 99 |
(5)如图所示,数轴上有四点A,B,C,D分别表示有理数a,b,c,d,用“<”把表示a,b,c,d,|a|,|b|,-|c|,-|d|的数连接起来.
分析:(1)首先根据非负数的性质求得a,b的值,然后a+b的值即可求解;
(2)①根据已知的式子可以转化成两个分式的差的形式;
②把每项化成两个分数的差的形式,然后即可求解;
(3)首先确定a,b的值,即可求解;
(4)首先去掉绝对值符号,然后相加即可求解;
(5)根据正数大于负数,两个负数绝对值大的反而小,即可确定.
(2)①根据已知的式子可以转化成两个分式的差的形式;
②把每项化成两个分数的差的形式,然后即可求解;
(3)首先确定a,b的值,即可求解;
(4)首先去掉绝对值符号,然后相加即可求解;
(5)根据正数大于负数,两个负数绝对值大的反而小,即可确定.
解答:解:(1)根据题意得:
,解得:
,则a+b=2-6=-4;
(2)①
=
-
;②原式=1-
+
-
+…-
=1-
=
;
(3)这两个点表示的数是±2和±3,
当两个数是2和3时,距离是1;
当两个数是-2和3时,距离是5;
当两个数是2和-3时,距离是5;
当两个数是-2,-3时,距离是1;
(4)原式=1-
+
-
+…+
-
=1-
=
;
(5)a<-|d|<-|c|<b<|b|<c<d<|a|.
|
|
(2)①
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2007 |
| 1 |
| 2007 |
| 2006 |
| 2007 |
(3)这两个点表示的数是±2和±3,
当两个数是2和3时,距离是1;
当两个数是-2和3时,距离是5;
当两个数是2和-3时,距离是5;
当两个数是-2,-3时,距离是1;
(4)原式=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 99 |
| 1 |
| 100 |
| 1 |
| 100 |
| 99 |
| 100 |
(5)a<-|d|<-|c|<b<|b|<c<d<|a|.
点评:本题考查了有理数的混合运算,正确理解已知中的式子的变形,读懂题目是关键.

练习册系列答案
相关题目
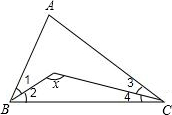 附加题:如图,已知∠1=∠2,∠3=∠4,∠A=100°,求x的值.
附加题:如图,已知∠1=∠2,∠3=∠4,∠A=100°,求x的值.
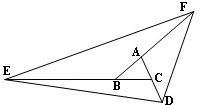 28、附加题:如图,已知△ABC的面积为1cm2,如果AD=2AC,BF=3BA,CE=4CB,求△DEF的面积.
28、附加题:如图,已知△ABC的面积为1cm2,如果AD=2AC,BF=3BA,CE=4CB,求△DEF的面积.