题目内容
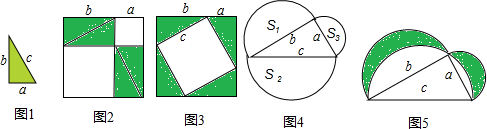
附加题:观察下列等式:
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
将以上三个等式两边分别相加得:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
(1)直接写出下列各式的计算结果:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
(2)猜想并写出:
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
(3)探究并解方程:
| 1 |
| x(x+3) |
| 1 |
| (x+3)(x+6) |
| 1 |
| (x+6)(x+9) |
| 3 |
| 2x+18 |
分析:(1)由等式:
=1-
,
=
-
,
=
-
,两边分别相加得:
+
+
=1-
+
-
+
-
=1-
=
,类比上面的做法得到答案;
(2)因
-
=
,再由
-
=
猜想出结论;
(3)由(2)的结论,可以推出
=
(
-
),进一步解出方程.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
(2)因
| 1 |
| n |
| 1 |
| n-2 |
| 2 |
| n(n+2) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n(n+1) |
(3)由(2)的结论,可以推出
| 1 |
| n(n+3) |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+3 |
解答:解:因为(1)
=1-
,
=
-
,
=
-
,
…
=
-
,
所以
+
+
+…+
,
=1-
+
-
+
-
+…+
-
,
=1-
,
=
;
(2)因为
-
=
,
所以
=
(
-
);
(3)类比(2)的结论,可以得到,
=
(
-
),
所以
+
+
=
,
(
-
+
-
+
-
)=
,
=
,
解得x1=-9,x2=2,
经检验,x1=-9是增根,x2=2是原方程的根.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
…
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
所以
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
(2)因为
| 1 |
| n |
| 1 |
| n-2 |
| 2 |
| n(n+2) |
所以
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
(3)类比(2)的结论,可以得到,
| 1 |
| n(n+3) |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+3 |
所以
| 1 |
| x(x+3) |
| 1 |
| (x+3)(x+6) |
| 1 |
| (x+6)(x+9) |
| 3 |
| 2x+18 |
| 1 |
| 3 |
| 1 |
| x |
| 1 |
| x+3 |
| 1 |
| x+3 |
| 1 |
| x+6 |
| 1 |
| x+6 |
| 1 |
| x+9 |
| 3 |
| 2x+18 |
| 3 |
| x(x+9) |
| 3 |
| 2x+18 |
解得x1=-9,x2=2,
经检验,x1=-9是增根,x2=2是原方程的根.
点评:解决此类问题,从特殊中找出一般情况,利用类比的思想进一步解决问题.

练习册系列答案
相关题目
 附加题:
附加题: ,
, ,
, ,
, .
.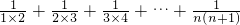 =______
=______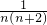 =
= (
( -
- ).
). .
.